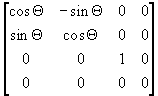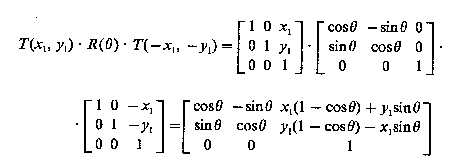Wyjaśnić pojęcie piksela.
Wyjaśnić pojęcie próbkowania obrazu.
Obliczyć pojemność pamięci potrzebna dla zapamiętania obrazu o rozdzielczości pikselowej
Określić czas transmisji obrazu z problemu 3, jeżeli przepustowość sieci wynosi 56 kb/s
Wyjaśnić zasadę wyświetlania rastrowego.
Uzasadnić konieczność stosowania przetworników cyfrowo-analogowych w torze wyświetlania z monitorem CRT.
Porównać metody wyświetlania barwnego piksela w monitorze CRT i w monitorze LCD.
Jak można rozwiązać problem wyświetlania obrazu na monitorze LCD jeżeli rozdzielczość pikselowa obrazu jest większa niż rozdzielczość monitora?
Proszę wyjaśnić od czego zależy obserwowana barwa obiektu.
Proszę omówić model percepcji barwy.
Co to są barwy monochromatyczne?
Czy za pomocą trzech barw podstawowych R, G i B można uzyskać dowolna barwę widzialną?
Proszę uzasadnić stwierdzenie: "model RGB wykorzystywany w grafice komputerowej ma budowę dyskretną"
Proszę podać ile różnych barw mamy do dyspozycji jeżeli piksel jest reprezentowany za pomocą słów odpowiednio 8-bitowych, 16-bitowych i 24-bitowych.
Proszę omówić wykres chromatyczności.
Proszę wyjaśnić przeznaczenie systemów zarządzania kolorami.
Wymienić podstawowe różnice między metodami modelowania: Brep, CSG i wokselową.
Naszkicować stożek oraz przykładową reprezentację wielokątową jego powierzchni bocznej.
Wyznaczyć wypadkową macierz dla operacji obrotu względem osi równoległej do osi z.
Korzystając z rysunku IX.7 zwrócić uwagę na wpływ oświetlenia na wygląd obiektu.
Wyjaśnić na czym polega różnica między cieniowaniem płaskim a cieniowaniem metodą Gouraud. Co można powiedzieć o złożoności obliczeniowej obu metod?
Podać jakie operacje trzeba wykonać, żeby uzyskać na ekranie obraz zielonej kostki sześciennej oświetlonej odległym źródłem światła
Zwrócić uwagę na dwa różne problemy, których rozwiązanie zaproponował Phong: cieniowanie powierzchni
Porównać metody odwzorowania tekstury: wprost i odwrotną.
Korzystając z algorytmu Bresenhama naszkicować na kratkowanym papierze odcinek o współrzędnych wierzchołków (2,3), (6,7)
Znaleźć czwarty piksel dla okręgu o środku w początku układu współrzędnych i promieniu r = 8.
Wyjaśnić skąd bierze się problem aliasingu i czy można jego efekty całkowicie wyeliminować.
Wyjaśnić koncepcję współrzędnych jednorodnych.
Znaleźć macierz przekształcenia dla operacji obejmującej przesunięcie trójkąta o wierzchołkach A(2,2), B(4,3), C(3,5) oraz obrót o kąt 45º względem przesuniętego wierzchołka A
Naszkicować krzywą Béziera określona przez następujące punkty sterujące: P0(2,2), P1(3,5), P2(6,6), P3(4,3).
Czy punkt o współrzędnych (1,4) może należeć do krzywej Béziera z problemu powyzej?
Wymienić podstawowe różnice między programami grafiki rastrowej i programami grafiki wektorowej.
W jaki sposób można rozwiązać problem określania kolejności wyświetlania obiektów. (nakładanie obektów)
Wyjaśnić na czym polega koncepcja przyciągania do linii siatki lub prowadnic
Wymienić podstawowe różnice między metodami modelowania: Brep, CSG i wokselową
Naszkicować stożek oraz przykładową reprezentację wielokątową jego powierzchni bocznej.
Wyjaśnić na czym polega problem kompresji i porównać metody kompresji bezstratnej i stratnej.
Wyjaśnić dlaczego w końcowej fazie kompresji metodą JPEG wykorzystuje się przeglądanie tablicy elementów metodą ZigZag.
Zaproponować prosty format pliku do pamiętania obrazów z odcieniami szarości. Założyć, że pamiętane będą obrazy o rozdzielczości 800 ´ 600 ´ 8.
Wymienić podstawowe cechy formatu PNG.
Czy korzystając z metody śledzenia promieni musimy wyznaczać bryłę widzenia?
Czy metoda śledzenia promieni rozwiązuje problem cieniowania? A jeżeli tak, to w jaki sposób?
W jaki sposób można znaleźć przecięcie promienia z kulą?
Zastanowić się na tym w jaki sposób można rozwiązać problem znajdowania pierwszej napotkanej bryły na drodze promienia biegnącego w stronę sceny zawierającej kilkadziesiąt brył.
Wymienić różne efekty, które mogą występować w ramach animacji.
Proszę wyjaśnić zasadę tworzenia klatek pośrednich.
Proszę wyjaśnić różnicę między warpingiem a morfingiem.
Zaproponować algorytm znajdowania odbicia lustrzanego obrazu w pionie.
Q: Wyjaśnić pojęcie piksela.
A: Najmniejszy jednolity element obrazu wyświetlanego na ekranie, drukowanego lub uzyskiwanego za pomocą urządzeń przetwarzania obrazu.
Q: Wyjaśnić pojęcie próbkowania obrazu.
A: Proces próbkowania obrazu można wyjaśnić poglądowo w następujący sposób. Wyobraźmy sobie, że na zdjęcie czarno-białe (przyjmujemy tu upraszczające założenie, że zdjęcie dobrej jakości odzwierciedla obraz rzeczywisty) nanosimy gęstą siatkę prostokątną. Każdy węzeł siatki odpowiada jednemu punktowi obrazu - jest próbką obrazu. Zbiór tak określonych próbek stanowi pewne przybliżenie obrazu. Każda próbka obrazu może przyjmować dowolną wartość z określonego przedziału jasności (odcieni szarości). Z kolei ten przedział wartości jest dzielony na pewną liczbę podprzedziałów i poszczególnym podprzedziałom przypisuje się różne kody cyfrowe. Stąd każdy kod cyfrowy reprezentuje określoną jasność (odcień szarości).
Q: Obliczyć pojemność pamięci potrzebna dla zapamiętania obrazu o rozdzielczości pikselowej 1024 x 768 x 24. Wynik proszę podać w megabajtach (MB)
A: 1024 * 768 * 24 = 18874368b == 2,25MB
Q: Określić czas transmisji obrazu z problemu 3, jeżeli przepustowość sieci wynosi 56 kb/s (to znaczy, że w ciągu sekundy można przesłać 56 kb informacji kodowanej dwójkowo).
A: 18874368b / 1000 (kilobit) = 18874,368 kb 18874,368 / 56 = 337,04 sek = 5,62 minut
Q: Wyjaśnić zasadę wyświetlania rastrowego.
A: Jest to sposób wyświetlania obrazu na urządzeniach zewnętrznych za pomocą siatki jednolitych punktów RGB.
Q: Uzasadnić konieczność stosowania przetworników cyfrowo-analogowych w torze wyświetlania z monitorem CRT.
A: Informacja o wyświetlanym obrazie jest pamiętana w pamięci obrazu w postaci cyfrowej. Natomiast z punktu widzenia monitora CRT potrzebna jest informacja w postaci napięcia, a więc w postaci analogowej. Stąd należy pamiętać, że w torze między pamięcią obrazu a monitorem CRT musi znajdować się przetwornik cyfrowo-analogowy (CA) dokonujący odpowiedniej konwersji postaci cyfrowej na wymaganą postać analogową. W praktyce są to trzy przetworniki dokonujące odpowiednio konwersji dla składowych R, G i B.
Q: Porównać metody wyświetlania barwnego piksela w monitorze CRT i w monitorze LCD.
A: W monitorze CRT kolorowy piksel jest reprezentowany poprzez odpowiednie pobudzenie luminosforów (one świecą) w kolorach RGB tak aby ich addytywna mieszanina dała docelowy kolor. W monitorze LCD zasada działania elementu wyświetlającego sprowadza się do tego, że zmiany zewnętrznego pola elektrycznego powodują zmiany orientacji molekuł w ciekłym krysztale, a w konsekwencji zmiany stanu tłumienia światła przez ciekły kryształ (między stanem przepuszczania i stanem blokowania światła). Ciekłe kryształy blokują bądź przepuszczają światło i nie wnoszą niczego jeśli chodzi o barwę. Stąd, w celu uzyskania barwnych pikseli, elementy wyświetlające pokrywa się filtrami kolorowymi i wykorzystuje się źródła światła białego.
Q: Jak można rozwiązać problem wyświetlania obrazu na monitorze LCD jeżeli rozdzielczość pikselowa obrazu jest większa niż rozdzielczość monitora? Dla przykładu założyć, że rozdzielczość obrazu wynosi 1024 ´ 768 a rozdzielczość monitora wynosi 800 ´ 600.
A: Problem można rozwiązać na 2 sposoby: pierwsze rozwiązanie to konwersja do rozdzielczości danego monitora, drugie to wyświetlenie tylko części ekranu i programowo przesuwać widzialną część razem z kursorem.
Q: Proszę wyjaśnić od czego zależy obserwowana barwa obiektu.
A: Składa się kilka czynników: charakterystyka źródła światła, charakterystyki odbicia lub transmisji dla obserwowanego obiektu, charakterystyki czułości poszczególnych receptorów (wszystkie charakterystyki w funkcji długości fali świetlnej). W mózgu następuje ostateczna interpretacja docierającej informacji i identyfikacja postrzeganego koloru obiektu.
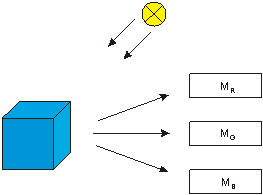
Q: Proszę omówić model percepcji barwy.
A: Światło odbite od obiektu pada na trzy rodzaje receptorów. Każdy z nich generuje pewną odpowiedź MR, MG i MB. Suma tych odpowiedzi określa postrzeganą barwę. Poszczególne receptory występujące w tym modelu określa się jako receptory RGB.
Q: Co to są barwy monochromatyczne?
A: Barwy monochromatyczne to takie barwy które związane są tylko z jedną długością fali.
Q: Czy za pomocą trzech barw podstawowych R, G i B można uzyskać dowolna barwę widzialną?
A: Nie można. Rzeczywistość jest bardziej złożona i w praktyce nie jest możliwe dobranie takich trzech barw podstawowych, które pozwalałyby reprodukować dowolne barwy.
Q: Proszę uzasadnić stwierdzenie: "model RGB wykorzystywany w grafice komputerowej ma budowę dyskretną".
A: Nie wiem...
Q: Proszę podać ile różnych barw mamy do dyspozycji jeżeli piksel jest reprezentowany za pomocą słów odpowiednio 8-bitowych, 16-bitowych i 24-bitowych.
A: 8-bitowe: 2^8 = 256 kolorów, 16-bitowe: 2^16 = 65536 kolorów, 24-bitowe: 2^24 = 16777216
Q: Proszę omówić wykres chromatyczności.
A: Wykres ten razem z luminancją Y pozwala dobrze opisywać różne barwy. W wykresie chromatyczności na części krzywoliniowej obwodu znajdują się wszystkie barwy widmowe nasycone. Na odcinku w dolnej części wykresu znajdują się purpury. W środkowej części wykresu znajduje się punkt W reprezentujący barwę białą. We wnętrzu wykresu znajdują się barwy nienasycone. Przedstawiony wykres chromatyczności jest przekrojem modelu trójwymiarowego dla ustalonej wartości Y. Cały model reprezentuje wszystkie barwy widzialne.
Q: Proszę wyjaśnić przeznaczenie systemów zarządzania kolorami.
A: System zarządzania kolorem ma za zadanie zarządzanie profilami oraz przesyłanie obrazów między urządzeniami z uwzględnieniem profili. Trzeba jednak pamiętać, że nie ma jednego uniwersalnego sposobu dokonywania transformacji kolorów jeżeli gamy kolorów urządzeń nie są identyczne. Stąd, mimo wszystko, trzeba liczyć się z tym, że mogą występować różnice przy reprodukcji obrazów w różnych systemach. Sytuację komplikuje dodatkowo fakt, iż najczęściej stosowana w praktyce przestrzeń L*a*b* nie uwzględnia w pełni warunków obserwacji obrazu.
Q: Wymienić podstawowe różnice między metodami modelowania: Brep, CSG i wokselową.
A:
Brep: Brep (ang. boundary representation) jest metodą brzegowej reprezentacji obiektów 3D. W większości zastosowań do opisania powierzchni zewnętrznej wykorzystuje się reprezentację wielokątową - powierzchnia boczna bryły jest opisywana za pomocą zbioru wielokątów. W przypadku takich brył jak wielościany reprezentacja ta jest w pełni naturalna. W przypadku gdy powierzchnie boczne nie są płaskie dokonuje się aproksymacji wielokątowej tych powierzchni. W niektórych zastosowaniach, gdzie zależy nam na jak największym realizmie generowanych obrazów, powierzchnie boczne złożonych obiektów opisuje się za pomocą odpowiednich powierzchni krzywoliniowych (na przykład powierzchni Béziera albo powierzchni NURBs (ang. nonuniform rational B-splines)).
CSG: W metodzie tej zakłada się, że dostępny jest zestaw podstawowych brył (tak zwanych prymitywów), z których można tworzyć bryły bardziej złożone. Wykorzystuje się przy tym operację łączenia brył ze sobą, operację znajdowania części wspólnej brył oraz operację odejmowania brył.
Metoda wokseolowa: W metodzie tej wykorzystuje się pojęcie woksela. Woksel jest to elementarna objętość w przestrzeni 3D, reprezentowana najczęściej jako najmniejszy sześcian, którym operujemy w fazie modelowania. Woksel można traktować jako komórkę rastra przestrzennego - przestrzenny odpowiednik piksela na płaszczyźnie. Modelowanie obiektu 3D sprowadza się do określenia zbioru wokseli należących do obiektu. Metoda wokselowa jest bardzo wymagająca jeśli chodzi o pojemność pamięci potrzebnej do zapamiętania informacji o obiekcie.
Q: Naszkicować stożek oraz przykładową reprezentację wielokątową jego powierzchni bocznej.
A:
Q: Wyznaczyć wypadkową macierz dla operacji obrotu względem osi równoległej do osi z.
A:
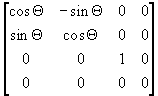
Q: Korzystając z rysunku IX.7 zwrócić uwagę na wpływ oświetlenia na wygląd obiektu.
A:



W zależności od oświetlenia użytkownik różnie odbiera wygląd obiektu 3D. Na pierwszym obrazku widzimy proste oświetlenie, przez które obiekt wygląda na płaski, jego ściany pokryte są jednolitym kolorem. Na pozostałych dwóch obrazkach ukierunkowany strumień swiatła pada na obiekty, tworząc efekt głębi obiektu.
Q: Wyjaśnić na czym polega różnica między cieniowaniem płaskim a cieniowaniem metodą Gouraud. Co można powiedzieć o złożoności obliczeniowej obu metod?
A: Cieniowanie Płaskie: Polega ona na określaniu jasności każdej ściany modelowanej bryły, opierając się na kącie pomiędzy powierzchnią ściany a kierunkiem światła, uwzględniając kolor ściany i oświetlenia oraz intensywność światła. Podstawową zaletą cieniowania płaskiego jest wysoka prędkość renderingu. Ponadto wypełnianie wielokątów jednym kolorem jest bardzo szybkie, nawet w komputerach nie posiadających akceleratorów graficznych. Wadą cieniowania jest to, że każda ściana modelu ma jednolitą barwę, co sprawia wrażenie występowania kantów i płaskich powierzchni; jest to tym bardziej zauważalne, im mniej złożony jest model.
Cieniowanie Gouraud: polega na przypisywaniu punktom cieniowanego wielokąta jasności obliczonej poprzez interpolację wartości odpowiednich dla każdego wierzchołka (w odróżnieniu od cieniowania Phonga, polegającego na interpolacji wektora normalnego). W odróżnieniu cieniowania płaskiego cieniowanie Gourauda zapewnia płynną zmianę stopnia jasności całego obiektu. Pewnym ograniczeniem metody Gouraud jest to, że zestaw barw jakie można uzyskać wewnątrz wypełnianego trójkąta jest ograniczony przez zestaw barw wierzchołkowych i na przykład nie można uzyskać efektu rozświetlenia wewnątrz trójkąta.
Q: Podać jakie operacje trzeba wykonać, żeby uzyskać na ekranie obraz zielonej kostki sześciennej oświetlonej odległym źródłem światła (promienie światła są do siebie równoległe). Obserwator może znajdować się w dowolnym punkcie poza sześcianem.
A: Według mnie: stworzyć model BREP kostki sześciennej, stworzyć materiał koloru zielonego i przypisać go ściankom modelu kostki, stworzyć światło punktowe z oddali od kostki, tak aby promienie podchodzące do kostki były niemal równoległe. Umieścić finalnie kamerę na scenie. Wykonać rzutowanie kostki na ekran w trybie perspektywicznym, za pomocą wektorów normalnych ścianek modelu kostki wyznaczyć widzialne ścianki, po czym zastosować cieniowanie płaskie do wykonania cieniowania ścianek kostki i narysować finalny obraz na ekranie monitora.
Q: Zwrócić uwagę na dwa różne problemy, których rozwiązanie zaproponował Phong: cieniowanie powierzchni wielokąta po zrzutowaniu na płaszczyznę metodą Phonga oraz wyznaczanie barwy punktu powierzchni 3D za pomocą równania Phonga.
A: 3===> w dupe!
Q: Porównać metody odwzorowania tekstury: wprost i odwrotną.
A: Odwzorowanie tekstury wprost: Przyjrzyjmy się problemowi odwzorowania z punktu widzenia pojedynczych pikseli. W ogólnym przypadku może wystąpić taka sytuacje, że po odwzorowaniu tekseli na docelową powierzchnię, pojedynczy piksel zostanie przykryty przez kilka tekseli. Wtedy barwę piksela trzeba wyznaczyć biorąc pod uwagę wielkość wpływu każdego z tekseli przykrywających piksel.
Odwzorowanie tekstury odwrotnie:Odwzorowuje się piksel na powierzchnię tekstury i barwę piksela określa się biorąc pod uwagę teksele, które znajdą się w obrębie obszaru reprezentującego piksel.
Q: Korzystając z algorytmu Bresenhama naszkicować na kratkowanym papierze odcinek o współrzędnych wierzchołków (2,3), (6,7) oraz odcinek o współrzędnych wierzchołków (2,3), (4,8).
A: Wybieramy koniec odcinka o mniejszej współrzędnej x. (algorytm nie zawsze podaje takie same wyniki i dlatego zawsze bierzemy koniec z mniejszym X). Wybrano (x0,y0).
Obliczyć pomocnicze wielkości:
Δx = x2 - x1, Δy = y2 - y1, a = 2Δy, b = 2Δy - 2Δx
oraz wartość początkową pomocniczego parametru decyzyjnego jako
p0 = 2Δy - Δx.
Dla kolejnych kolum o współrzędnych xk, zaczynając od k = 0 sprawdzić znak wartości pomocniczego parametru pk.
W przypadku gdy pk < 0 następny piksel ma współrzędne (xk+1, yk) i nowa wartość parametru decyzyjnego jest określana z zależności pk+1 = pk + a.
W przeciwnym przypadku następny punkt ma współrzędne (xk+1, yk+1) i nowa wartość parametru decyzyjnego jest określana z zależności pk+1 = pk + b.
Krok 3 jest powtarzany dopóki nie dojdziemy do końca odcinka.
Przykład
Korzystając z metody Bresenhama znaleźć kolejne piksele dla odcinka o współrzędnych końców (2,2), (8,5).
Wybieramy pierwszy punkt odcinka. Jest to punkt (2,2).
Obliczamy pomocnicze wielkości
Δx = 8 - 2 = 6 Δy = 5 - 2 = 3 a = 2 * 3 = 6 b = 6 - 12 = -6
p0 = 2Δy - Δx = 6 - 6 = 0
Wyznaczamy kolejne piksele
Ponieważ p0 = 0, to następny piksel ma współrzędne (3,3) i
p1 = p0 + b = 0 - 6 = -6
Ponieważ p1 < 0, to następny piksel ma współrzędne (4,3) i
p2 = p1 + a = -6 + 6 = 0
Ponieważ p2 = 0, to następny piksel ma współrzędne (5,4) i
p3 = p2 + b = 0 - 6 = -6
itd. Cały odcinek pokazano na rysunku VI.5.
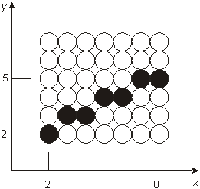
Q: Znaleźć czwarty piksel dla okręgu o środku w początku układu współrzędnych i promieniu r = 8.
1. Punkt początkowy ma współrzędne (0, r). Natomiast początkowa wartość pomocniczego parametru decyzyjnego wynosi P0=(5/4)-r
2. Dla kolejnych kolumn o współrzędnych xk, zaczynając od k = 0, należy sprawdzić znak wartości pomocniczego parametru pk.
W przypadku gdy pk < 0, następny piksel ma współrzędne (xk+1, yk) i nowa wartość parametru decyzyjnego jest określana z zależności
pk+1 = pk +2xk+1 +1.
W przeciwnym przypadku, następny punkt ma współrzędne (xk+1, yk-1) i nowa wartość parametru decyzyjnego jest określana z zależności
pk+1 = pk + 2xk+1 +1 - 2yk+1.
3. Wyznaczyć siedem pikseli o współrzędnych wynikających z właściwości symetrii okręgu.
4. Powtarzać kroki 2 i 3 do czasu gdy spełniony będzie warunek x = y.
Q: Wyjaśnić skąd bierze się problem aliasingu i czy można jego efekty całkowicie wyeliminować.
A: Aliasing w grafice komputerowej to zjawisko zniekształcenia obrazu w wyniku zbyt małej częstości jego próbkowania w procesie rasteryzacji. Rasteryzacja ta zachodzi najczęściej podczas wyświetlania obrazu na ekranie, który obecnie najczęściej jest ekranem rastrowym, ale może dotyczyć także procesu zamiany modelu opisu obrazu z wektorowego na rastrowy.
Aby zminimalizować ten efekt stosuje się tzw. antyaliasing, który powoduje jednak, że obraz staje się w pewnym stopniu nieostry.
Q: Wyjaśnić koncepcję współrzędnych jednorodnych.
A: Współrzędne jednorodne to sposób reprezentacji punktów n-wymiarowych za pomocą n + 1 współrzędnych. Maxwell użył ich do rozwiązywania problemów związanych z rzutowaniem.
Punkt w przestrzeni dwuwymiarowej (na płaszczyźnie) opisuje para liczb (x,y), we współrzędnych jednorodnych trójka (x,y,W); podobnie punkt trójwymiarowy we współrzędnych jednorodnych reprezentuje czwórka (x,y,z,W), itd. - Przejście do współrzędnych jednorodnych umożliwia jednolity zapis podstawowych przekształceń geometrycznych: przesunięcia, obrotu, skalowania i innych za pomocą macierzy przekształceń 3x3. Pozwala to realizować takie operacje za pomocą specjalizowanego sprzętu i w efekcie przyspieszanie obliczeń.
Q: Znaleźć macierz przekształcenia dla operacji obejmującej przesunięcie trójkąta o wierzchołkach A(2,2), B(4,3), C(3,5) oraz obrót o kąt 45º względem przesuniętego wierzchołka A.
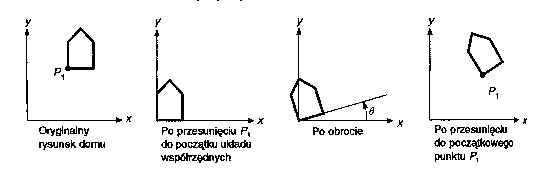
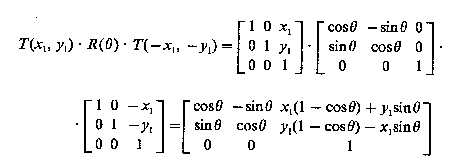
Q: Naszkicować krzywą Béziera określona przez następujące punkty sterujące: P0(2,2), P1(3,5), P2(6,6), P3(4,3).
A: do zrobienia
Q: Czy punkt o współrzędnych (1,4) może należeć do krzywej Béziera z problemu powyzej?
A: do zrobienia
Q: Wymienić podstawowe różnice między programami grafiki rastrowej i programami grafiki wektorowej.
A:
Rastrowe
- efektem pracy jest uzyskanie mapy pikselowej obrazu.
- każdy narysowany obiekt jest bezpośrednio umieszczany w mapie pikselowej i po narysowaniu przestaje być niezależnym obiektem, który może być dalej edytowany
- Edycji może podlegać cały obraz lub wybrany fragment mapy pikselowej ewentualnie dana warstwa
Wektorowe
-obiekt stanowi niezależną jednostkę i może być niezależnie edytowany (jesli zgrupujemy obiekty to wtedy cała grupa podlega educji)
Q: W jaki sposób można rozwiązać problem określania kolejności wyświetlania obiektów. (nakładanie obektów)
A: rysujemy je w odpowiedniej kolejności zaczynając od tego który jest na "spodzie".
Q: Wyjaśnić na czym polega koncepcja przyciągania do linii siatki lub prowadnic
A: wokół przyciągającego obiektu tworzy się umowne pole. Każdy obiekt, który znajdzie się w tym polu jest przyciągany do obiektu przyciągającego.
Q: Wymienić podstawowe różnice między metodami modelowania: Brep, CSG i wokselową
A:
BREP (ang. boundary representation): Modelowanie szkieletowe - stanowi często podstawę dla utworzenia bardziej szczegółowego modelu, w którym opisuje się powierzchnię zewnętrzną obiektu.
CSG (ang. constructive solid geometry): zakłada się, że dostępny jest zestaw podstawowych brył (tak zwanych prymitywów), z których można tworzyć bryły bardziej złożone. Wykorzystuje się przy tym operację łączenia brył ze sobą, operację znajdowania części wspólnej brył oraz operację odejmowania brył.
WOKSELOWA:umożliwia reprezentowanie całej bryły a nie tylko jej powierzchni zewnętrznej.Woksel jest to elementarna objętość w przestrzeni 3D, reprezentowana najczęściej jako najmniejszy sześcian, którym operujemy w fazie modelowania. Woksel można traktować jako komórkę rastra przestrzennego - przestrzenny odpowiednik piksela na płaszczyźnie. Modelowanie obiektu 3D sprowadza się do określenia zbioru wokseli należących do obiektu.
metoda bardzo wymagająca pamięciowo, do każdego woksela mozemy przypisać odpowiednie wartości atrybutów (np. czy woksel to tkanka miekka, czy kośc czy mięsień, itp.)
PRZESUWANIE (ang. sweeping): - definiowany jest przekrój bryły, który następnie jest przesuwany wzdłuż zadanej ścieżki. W czasie przesuwania jest wyznaczana powierzchnia boczna bryły. Ścieżka może być linią prostą albo krzywą (na przykład krzywą Béziera). W czasie przesuwania przekrój bryły może się zmieniać. W szczególnym przypadku, gdy przekrój jest obracany wokół pewnej osi możliwe jest tworzenie brył obrotowych
Q: Naszkicować stożek oraz przykładową reprezentację wielokątową jego powierzchni bocznej.
A: do zrobienia na tablicy
Q: Wyjaśnić na czym polega problem kompresji i porównać metody kompresji bezstratnej i stratnej.
A: Gotowe obrazy są pamiętane w postaci map bitowych. Przy obecnie stosowanych rozdzielczościach obrazów 800 ´ 600, 1024 x 768 czy 1280 ´ 1024 i 24 bitach na piksel ilość miejsca w pamięci potrzebna na zapisanie pojedynczego obrazu jest znaczna (odpowiednio w przybliżeniu 1,44 MB, 2,36 MB, 3,93 MB). Dodatkowy problem pojawia się przy przesyłaniu obrazów - czas transmisji jest odpowiednio długi. Stąd pojawia się potrzeba stosowania kompresji obrazów, a więc zapisywania ich w takiej postaci, żeby możliwie maksymalnie zmniejszyć ilość pamięci potrzebnej do zapamiętania obrazu.
Bezstratna - obraz poddany kompresji, a następnie dekompresji będzie wyglądał dokładnie tak samo jak obraz pierwotny - w czasie procesu kompresja-dekompresja nie jest tracona żadna informacja. Założenie to istotnie ogranicza możliwość uzyskania wysokiej kompresji. W praktyce, metody bezstratne pozwalają uzyskiwać stopnie kompresji (stosunek wymaganej pojemności pamięci przed kompresją do wymaganej pojemności po kompresji) rzędu kilku.
Stratna - Dopuszczalna jest utrata części pamięci. można uzyskiwać wysokie stopnie kompresji rzędu kilkudziesięciu. W metodach realizujących kompresję stratną z reguły dąży się do usuwania informacji mających stosunkowo małe znaczenie dla interpretacji całego obrazu, a więc dąży się do usuwania mało istotnych szczegółów.
Q: Wyjaśnić dlaczego w końcowej fazie kompresji metodą JPEG wykorzystuje się przeglądanie tablicy elementów metodą ZigZag.
A: Taki porządek jest przyjęty ze względu na to, że pozwala uzyskać długi ciąg zer zgrupowanych w prawej dolnej części tablicy. Zauważmy, że do ciągu nie wchodzi element z lewego górnego rogu oznaczony jako DC. Jest on kodowany wspólnie z odpowiednimi elementami dla innych bloków obrazu 8x8, z których składa się cały obraz poddawany kompresji.
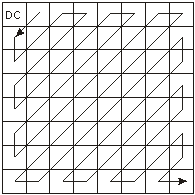
Q: Zaproponować prosty format pliku do pamiętania obrazów z odcieniami szarości. Założyć, że pamiętane będą obrazy o rozdzielczości 800 ´ 600 ´ 8.
A: PNG?
Q:Wymienić podstawowe cechy formatu PNG.
A: Format ten zapewnia dobrą kompresję bezstratną, nie jest objęty żadnymi zastrzeżeniami patentowymi i stąd coraz częściej wypiera format GIF.
Q:Czy korzystając z metody śledzenia promieni musimy wyznaczać bryłę widzenia?
A: Nie
Q:Czy metoda śledzenia promieni rozwiązuje problem cieniowania? A jeżeli tak, to w jaki sposób?
A: Tak. Śledzenie promieni dla każdego piksela na ekranie prowadzi promień w głąb ekranu zgodnie z perspektywą i natrafia na konkretne miejsce obiektu, dla którego musi wyznaczyć wektory normalne i wektory światła, dzięki czemu można wyznaczyć jasność tego piksela.
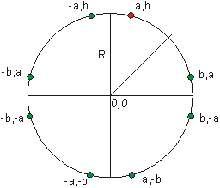
Q:W jaki sposób można znaleźć przecięcie promienia z kulą? (Zagadnienie to nie było omawiane w wykładzie, ale po przypomnieniu sobie wykładów z matematyki nie powinno nastręczać kłopotów.)
A: Jeżeli prowadzony promień znajduje się od punktu X,Y który jest środkiem kuli, w odległości mniejszej niż R to sygnalizuje przecięcie z kulą. Żeby znaleźć przecięcia musimy znaleźć takie punkty na prostej, żeby ich odległość od środka kuli była równa r.
Q: Zastanowić się na tym w jaki sposób można rozwiązać problem znajdowania pierwszej napotkanej bryły na drodze promienia biegnącego w stronę sceny zawierającej kilkadziesiąt brył.
A:???
Q:Wymienić różne efekty, które mogą występować w ramach animacji.
A:Przesunięcie, skalowanie, morffing, wraping, rotacja, zmiana materiału
Q: Proszę wyjaśnić zasadę tworzenia klatek pośrednich.
A:Klatki pośrednie SA to automatycznie wygenerowane przez odpowiedni algorytm, na podstawie stanu obiektu zawartego w klatkach kluczowych. Przykładowym algorytmem może być Interpolacja
Q:Proszę wyjaśnić różnicę między warpingiem a morfingiem.
Wrapinng polega na zmianie kształtu (deformacji) obiektu za pomocą np. rozciągania, a morfing polega na przekształcaniu jednego obiektu w drugi.
Q:Zaproponować algorytm znajdowania odbicia lustrzanego obrazu w pionie.
A:???
Q: Wyjaśnić na czym polega zadanie pseudokolorowania.
Tworzymy tablicę, w której mamy wytyczone barwy pierwotne oraz paletę barw które mają być zamienione. Tworzymy tablice barw na które chcemy zamienić wytyczone barwy. Następnie przechodzimy po wszystkich pikselach i zamieniamy w przypadku natrafienia na wytyczoną barwę na barwę na którą chcemy zamienić.
Q:Wyjaśnić pojęcie histogramu obrazu. Proszę również znaleźć histogram dla obrazu pokazanego na rysunku. W obrazie wykorzystano 6 różnych barw.
PRZYKŁADY Z WYKŁADU
Obliczanie realnych wielkości obrazka cyfrowego przy reprezentacji w konkretnym dpi
Jakie będą rozmiary obrazu o rozdzielczości pikselowej 800 ´ 600 reprodukowanego na drukarce o rozdzielczości a) 300 dpi, b) 600 dpi?
W przypadku a) wymiary obrazu będą wynosiły odpowiednio:
800/300 = 2,66" = 6,77 cm i 600/300 = 2" = 4,08 cm.
W przypadku b) otrzymamy odpowiednio:
800/600 = 1,33" = 3,39 cm i 600/600 = 1" = 2,54 cm.
Wyliczanie rozdzielczości liniowej w poziomie
Dla ekranu o rozdzielczości 800 ´ 600 pikseli i przekątnej 15" określić rozdzielczość liniową w poziomie wyrażoną w dpi. Przyjąć, że stosunek boków ekranu wynosi a : b = 4 : 3.
Z równania Pitagorasa mamy, że 15^2 = a^2 + b^2. Wprowadzając pomocniczą zmienną x możemy boki kwadratu zapisać w postaci a = 4x oraz b = 3x. Po podstawieniu do równania i rozwiązaniu otrzymujemy, że x = 3". Stąd a = 12" i b = 9". Wobec tego szukana rozdzielczości w poziomie wynosi 800/12" = 66,6 dpi.
Obliczanie rozmiaru obrazów
Za pomocą dwóch urządzeń uzyskano obrazy o rozmiarach 2" ´ 2". Określić wymaganą pojemność pamięci dla przechowania obrazów jeżeli poszczególne urządzenia miały następujące parametry: a) rozdzielczość liniowa 72 dpi, obraz czarno-biały 1 bit/piksel, b) rozdzielczość liniowa 300 dpi, obraz kolorowy 24 bity/piksel. Zakładamy, że przechowujemy tylko informacje o pikselach obrazu.
W przypadku a) potrzebna jest pamięć o pojemności:
(2 * 72) * (2 * 72) * 1 = 2,592 kB
W przypadku b) potrzebna jest pamięć o pojemności:
(2 * 300) * (2 * 300) * 24 = 1,08 MB
Obliczanie ilości rozróżnialnych pikseli
Obserwator ogląda obraz o szerokości 30 cm z odległości 50 cm. Przyjmując, że obserwator jest w stanie rozróżniać szczegóły widziane w obrębie kąta o wartości 1 minuty kątowej (1') określić przybliżoną liczbę pikseli w poziomie, które obserwator jest w stanie rozróżnić.
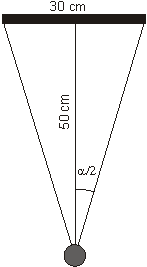
Korzystając z rysunku pokazanego obok możemy zapisać, że tg a/2 =0,3. Stąd a/2 @ 17° i a @ 34°. Przy założonej zdolności rozróżniania szczegółów i pamiętając, że 1° = 60' otrzymujemy szukany wynik: 34 * 60 = 2040 pikseli.
Obliczenia czasu dla generowania jednego piksela
Załóżmy, że monitor ma rozdzielczość 1024 ´ 768 pikseli oraz, że częstotliwość odświeżania wynosi 85 Hz. Przyjmijmy dodatkowo, że czas powrotu plamki w poziomie wynosi 4 m s a czas powrotu w pionie 40 m s. Należy obliczyć ile czasu jest do dyspozycji dla wyświetlenia jednego piksela.
Jeżeli częstotliwość odświeżania wynosi 85 Hz, to czas dostępny na wyświetlenie jednej ramki wynosi około 11,765 ms. W tym czasie muszą zostać wyświetlone wszystkie piksele (jest ich 1024 ´ 768) i musi nastąpić 767 powrotów poziomych oraz jeden powrót pionowy. Oznaczając czas dostępny na wyświetlenie jednego piksela przez x otrzymujemy, że:
11 765 m s = 1024 * 768 * x + 767 * 4 m s + 40 m s
Stąd:
x » 11 ns.
Metoda Bresenhama
Korzystając z metody Bresenhama znaleźć kolejne piksele dla odcinka o współrzędnych końców (2,2), (8,5).
Wybieramy pierwszy punkt odcinka. Jest to punkt (2,2).
Obliczamy pomocnicze wielkości
Δx = 8 - 2 = 6 Δy = 5 - 2 = 3 a = 2 * 3 = 6 b = 6 - 12 = -6
p0 = 2Δy - Δx = 6 - 6 = 0
Wyznaczamy kolejne piksele
Ponieważ p0 = 0, to następny piksel ma współrzędne (3,3) i
p1 = p0 + b = 0 - 6 = -6
Ponieważ p1 < 0, to następny piksel ma współrzędne (4,3) i
p2 = p1 + a = -6 + 6 = 0
Ponieważ p2 = 0, to następny piksel ma współrzędne (5,4) i
p3 = p2 + b = 0 - 6 = -6
Rysowanie okręgu
Algorytm rysowania okręgu o środku w początku układu współrzędnych i o promieniu r metodą z punktem środkowym wygląda następująco.
Punkt początkowy ma współrzędne (0, r). Natomiast początkowa wartość pomocniczego parametru decyzyjnego wynosi
Dla kolejnych kolumn o współrzędnych xk, zaczynając od k = 0, należy sprawdzić znak wartości pomocniczego parametru pk.
W przypadku gdy pk < 0, następny piksel ma współrzędne (xk+1, yk) i nowa wartość parametru decyzyjnego jest określana z zależności
pk+1 = pk +2xk+1 +1.
W przeciwnym przypadku, następny punkt ma współrzędne (xk+1, yk-1) i nowa wartość parametru decyzyjnego jest określana z zależności
pk+1 = pk + 2xk+1 +1 - 2yk+1.
Wyznaczyć siedem pikseli o współrzędnych wynikających z właściwości symetrii okręgu.
Powtarzać kroki 2 i 3 do czasu gdy spełniony będzie warunek x = y.
Obcinanie odcinków
Sprawdzić czy odcinki A i C z rysunku VII.8 można wyeliminować z dalszej procedury obcinania.
Końce odcinka A znajdują się w obszarach o kodach 1001 oraz 1000. Iloczyn tych kodów jest równy 1000, a więc jest różny od zera. Wobec tego odcinek może być wyeliminowany.
Końce odcinka C znajdują się w obszarach o kodach 1000 oraz 0010. Iloczyn tych kodów jest równy 0000, a więc jest równy zeru. Wobec tego odcinek nie może być wyeliminowany.
Odpowiedzi na pytania z podsumowania
1. Podstawowe algorytmy techniki rastrowej
a. Dwa przecinające się odcinki mogą mieć więcej niż jeden piksel wspólny
TAK
b. Odcinek o współrzędnych końców (2,1), (5,6) narysowany przy wykorzystaniu algorytmu Bresenhama składa się z 6 pikseli
TAK
c. Aliasing jest skutkiem skończonej rozdzielczości rastra
TAK
2. Barwa w grafice komputerowej
a. W modelu RGB, przy reprezentacji barwy za pomocą 24 bitów, barwa czarna ma współrzędne (255, 255, 255)
NIE
b. W systemie full color (pełnokolorowym) każda składowa barwy jest reprezentowana za pomocą 10 bitów
NIE
c. W modelu CIE XYZ barwy nasycone znajdują się na obwiedni wykresu chromatyczności we współrzędnych xy
NIE WIEM
3. Podstawowe przekształcenia geometryczne
a. Kwadrat o współrzędnych wierzchołków (0, 0), (1, 0), (1, 1), (0, 1) został poddany operacji skalowania ze współczynnikami Sx = 2, Sy = 3 i przesunięty o wektor (3, 2). Współrzędne jednego z wierzchołków otrzymanej figury to (2, 5)
NIE
b. Punkt o współrzędnych jednorodnych (5, 4, 3,1) w układzie współrzędnych xyz ma współrzędne (5, 4, 3)
NIE WIEM
c. W przekształceniu typu obrót, punkt wokół którego następuje obrót musi pokrywać się z początkiem układu współrzędnych
NIE