|
12 |
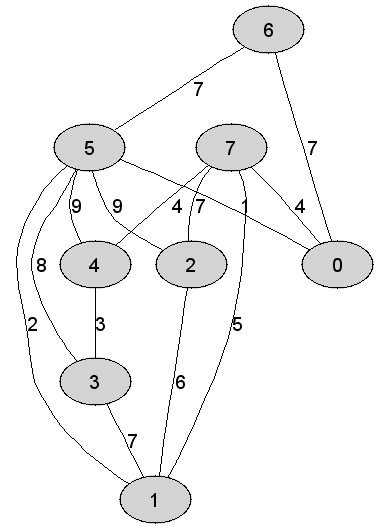
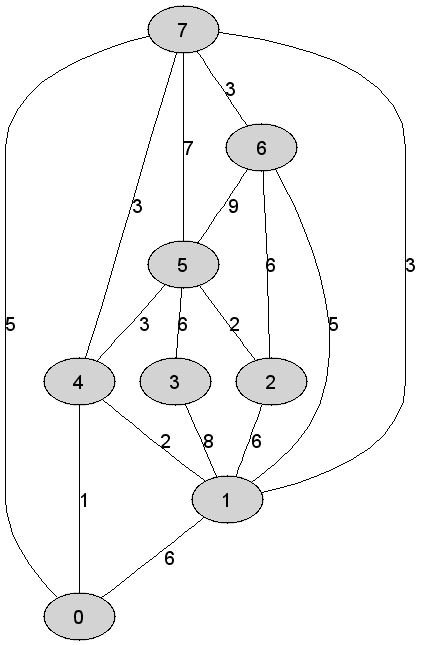
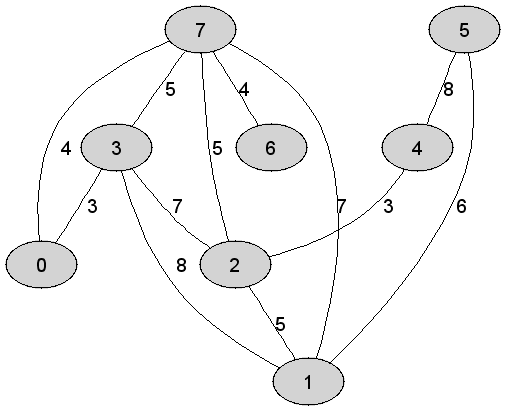
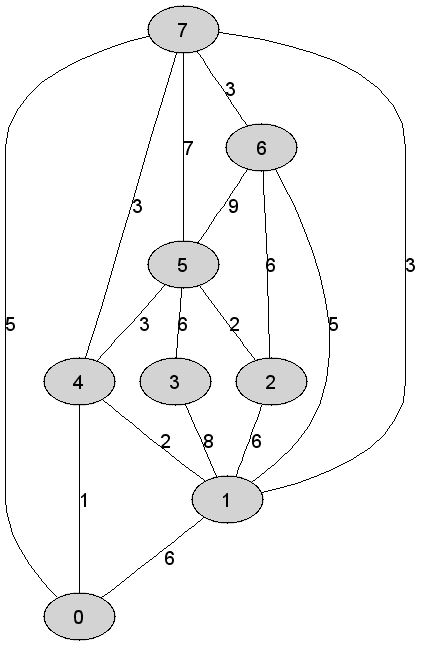
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, jeszcze przed ustaleniem jego
finalnej postaci, jest równa dokładnie |
0 |
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
|||
|
12 |
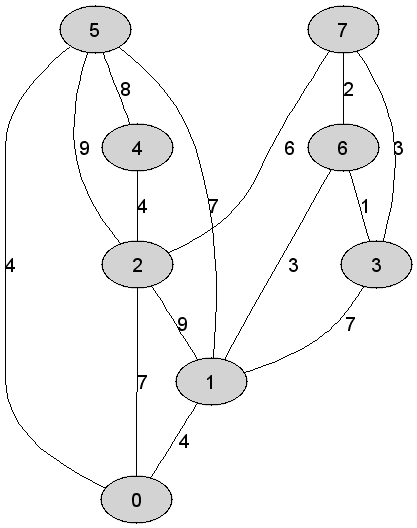
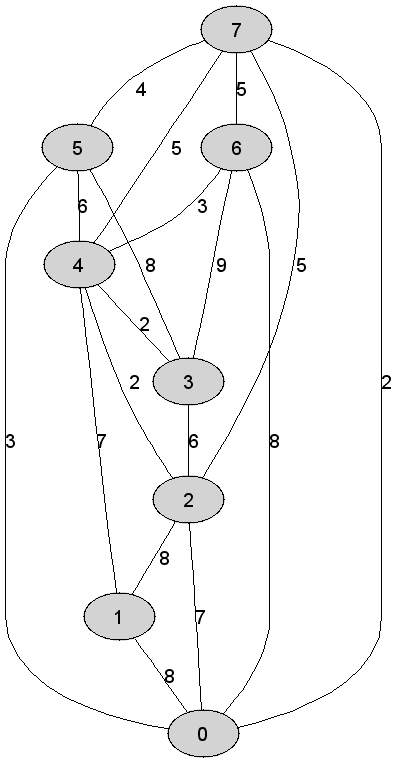
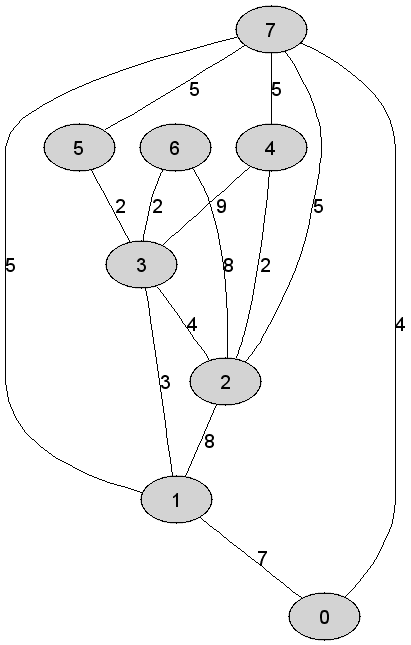
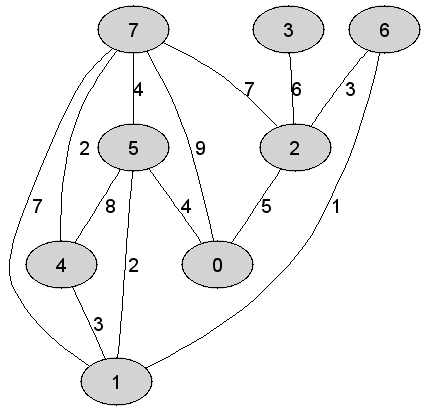
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej
postaci, jest równa dokładnie |
0 |
|||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej
postaci, jest równa dokładnie |
0 |
|||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej
postaci, jest równa dokładnie |
1 |
+ |
||
|
12 |
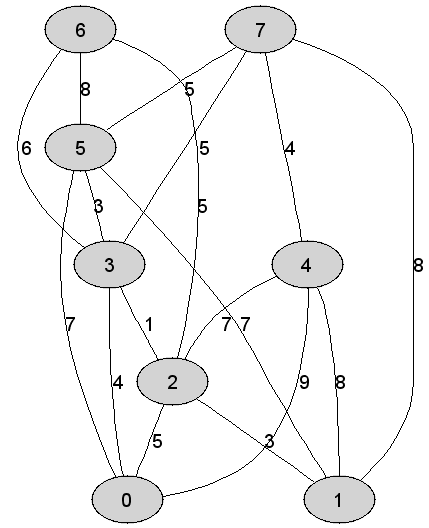
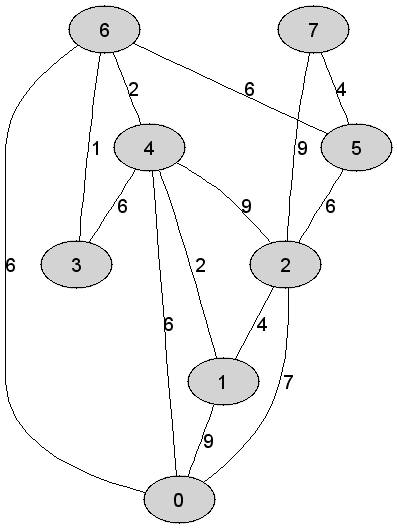
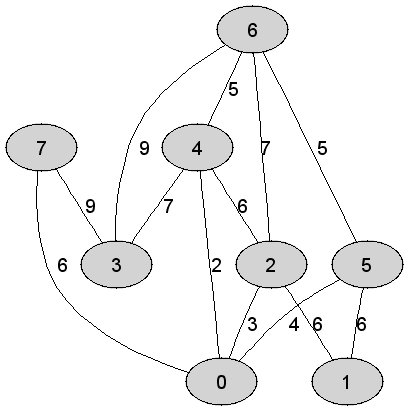
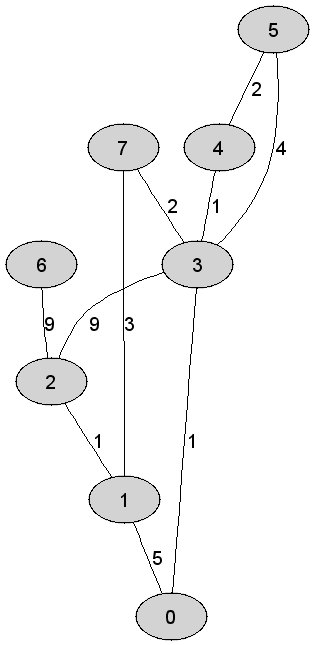
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
+ |
||
|
Kolejność
akceptowania krawędzi grafu do drzewa rozpinającego w trakcie wykonania
rozważanego algorytmu jest następująca: |
0 |
+ |
||
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
1 |
+ |
+ |
|
|
12 |
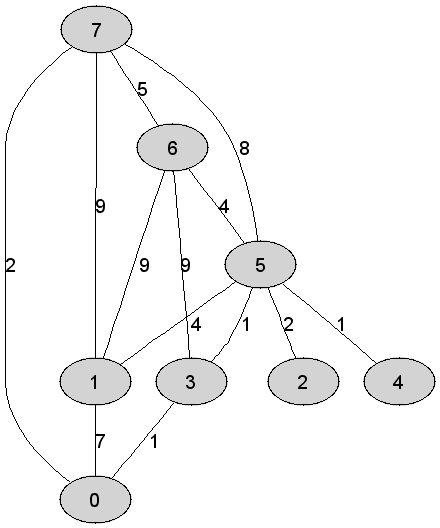
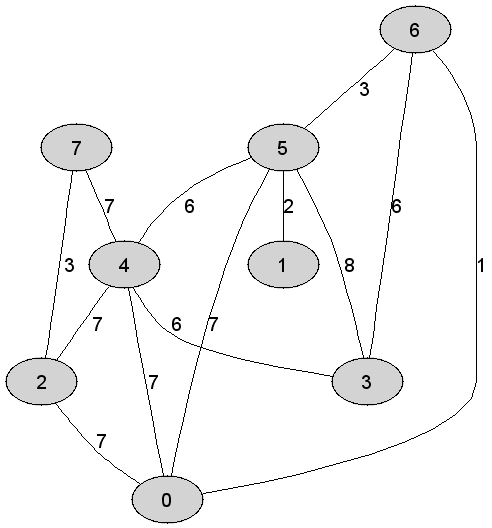
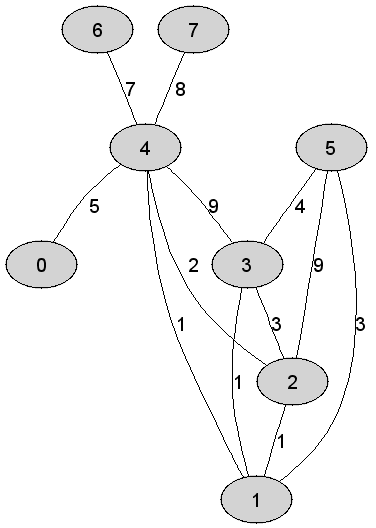
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
+ |
|
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
0 |
|||
|
Kolejność
akceptowania krawędzi grafu do drzewa rozpinającego w trakcie wykonania
rozważanego algorytmu jest następująca: |
0 |
|||
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
|
Suma wag krawędzi tworzących drzewo rozpinające
grafu |
0 |
|
|
|
|
Liczba krawędzi grafu odrzuconych (ze względu na
możliwość utworzenia cyklu) w trakcie konstrukcji drzewa rozpinającego,
jeszcze przed ustaleniem jego finalnej postaci, jest równa dokładnie |
1 |
+ |
|
|
|
Suma wag krawędzi tworzących drzewo rozpinające
grafu |
0 |
|
|
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
+ |
|
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
1 |
+ |
+ |
|
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
1 |
+ |
||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
12 |
Rozważmy nieskierowany graf prosty
|
|||
|
Maksymalna waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
+ |
|
|
Maksymalna waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
Liczba krawędzi grafu odrzuconych (ze względu na możliwość utworzenia
cyklu) w trakcie konstrukcji drzewa rozpinającego, jeszcze przed ustaleniem
jego finalnej postaci, jest równa dokładnie |
0 |
|||
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej
postaci, jest równa dokładnie |
1 |
+ |
||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej
postaci, jest równa dokładnie |
0 |
|||
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
0 |
|||
|
14 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
+ |
||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, jeszcze przed ustaleniem jego
finalnej postaci, jest równa dokładnie |
1 |
+ |
||
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, jeszcze przed ustaleniem jego
finalnej postaci, jest równa dokładnie |
1 |
+ |
||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, jeszcze przed ustaleniem jego
finalnej postaci, jest równa dokładnie |
0 |
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
14 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
akceptowania krawędzi grafu do drzewa rozpinającego w trakcie wykonania
rozważanego algorytmu jest następująca: |
0 |
|||
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
0 |
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
+ |
|
|
14 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
+ |
|
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
0 |
+ |
||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
|||
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
Suma wag
krawędzi tworzących drzewo rozpinające grafu |
0 |
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
12 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
0 |
+ |
||
|
Maksymalna
waga krawędzi tworzącej otrzymane drzewo rozpinające grafu |
1 |
+ |
||
|
Liczba
krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w
trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej
postaci, jest równa dokładnie |
1 |
+ |
||