|
8 |
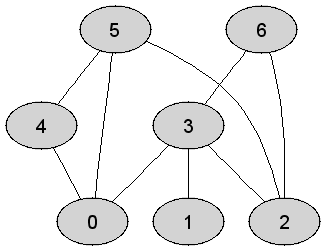
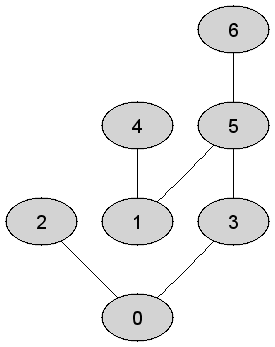
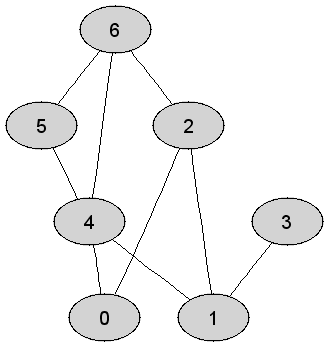
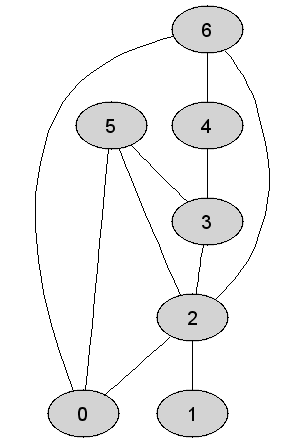
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu jest równa co
najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie
wykonania rozważnego algorytmu dla grafu |
1 |
+ |
||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu jest równa co
najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie
wykonania rozważnego algorytmu dla grafu |
1 |
+ |
||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
|||
|
8 |
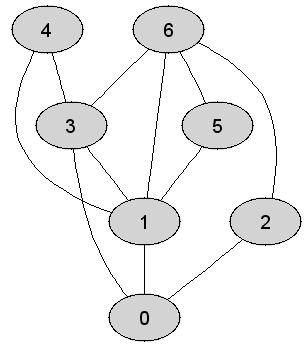
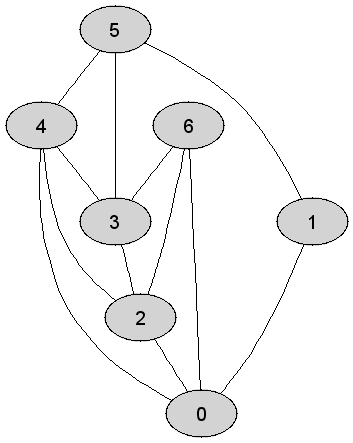
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
1 |
+ |
||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu jest równa co
najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie
wykonania rozważnego algorytmu dla grafu |
1 |
+ |
||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu jest równa co
najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie
wykonania rozważnego algorytmu dla grafu |
0 |
|||
|
8 |
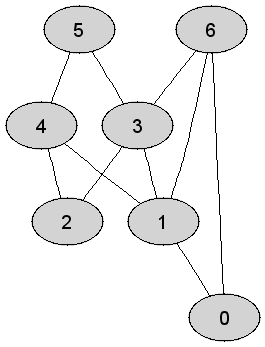
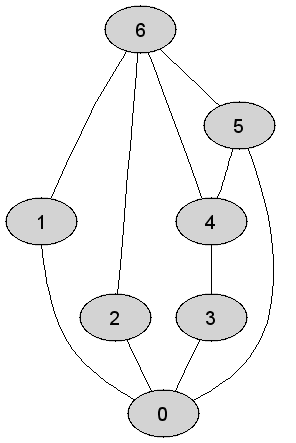
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
operacji POP w stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
1 |
+ |
+ |
|
|
Liczba operacji
PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest równa
dokładnie |
0 |
+ |
||
|
Kolejność
odwiedzenia wierzchołków jest następująca: |
0 |
+ |
||
|
8 |
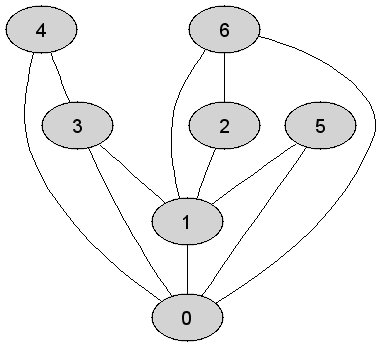
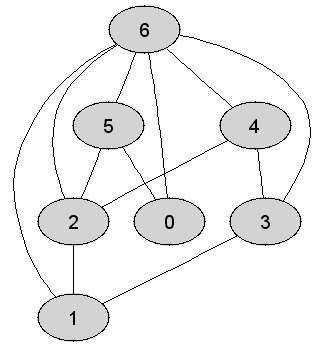
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
+ |
||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
1 |
+ |
||
|
Kolejność
odwiedzenia wierzchołków jest następująca: |
1 |
+ |
||
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
|
Liczba operacji OUT w stosie pomocniczym w trakcie
wykonania algorytmu DFS jest równa dokładnie |
0 |
|
|
|
|
Maksymalna wysokość stosu pomocniczego w trakcie
wykonania algorytmu jest równa co najwyżej maksymalnej wysokości stosu
pomocniczego, w trakacie wykonania rozważnego algorytmu dla grafu |
1 |
+ |
|
|
|
Maksymalna wysokość stosu pomocniczego w trakcie
wykonania algorytmu DFS jest równa dokładnie |
0 |
|
|
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu DFS jest równa
dokładnie |
0 |
|||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu jest równa co
najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie
wykonania rozważnego algorytmu dla grafu |
1 |
+ |
||
|
Kolejność
odwiedzenia wierzchołków jest następująca: |
0 |
+ |
||
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
|||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
|||
|
Kolejność
odwiedzenia wierzchołków jest następująca: |
1 |
+ |
||
|
|
||||
|
8 |
Rozważmy nieskierowany graf prosty
|
|||
|
Maksymalna wysokość stosu pomocniczego w trakcie wykonania algorytmu jest
równa co najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie wykonania rozważnego algorytmu dla grafu |
1 |
+ |
+ |
|
|
Liczba operacji POP w stosie pomocniczym w trakcie wykonania algorytmu
DFS jest równa dokładnie |
1 |
+ |
+ |
|
|
Liczba operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu
DFS jest równa dokładnie |
0 |
|||
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
odwiedzenia wierzchołków jest następująca: |
1 |
+ |
||
|
Liczba
operacji OUT w stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
|||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
|||
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu DFS jest równa
dokładnie |
1 |
+ |
||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu jest równa co
najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie
wykonania rozważnego algorytmu dla grafu |
1 |
+ |
||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
|||
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu DFS jest równa
dokładnie |
1 |
+ |
||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu jest równa co
najwyżej maksymalnej wysokości stosu pomocniczego, w trakacie
wykonania rozważnego algorytmu dla grafu |
0 |
|||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu DFS jest równa
dokładnie |
0 |
|||
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
0 |
|||
|
Kolejność
odwiedzenia wierzchołków jest następująca: |
1 |
+ |
||
|
Maksymalna
wysokość stosu pomocniczego w trakcie wykonania algorytmu DFS jest równa
dokładnie |
0 |
|||
|
8 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
operacji POP w stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
1 |
+ |
+ |
|
|
Kolejność
odwiedzenia wierzchołków jest następująca: |
0 |
|||
|
Liczba
operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest
równa dokładnie |
1 |
+ |
||