|
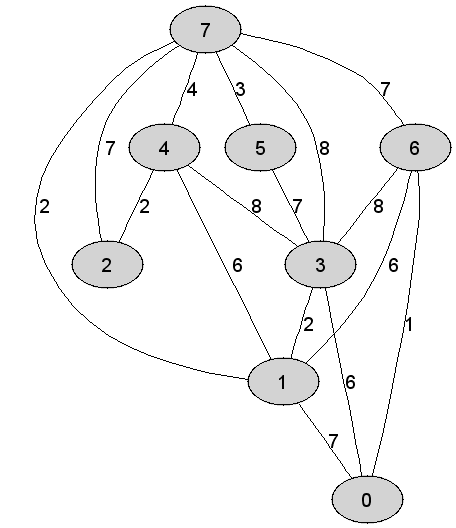
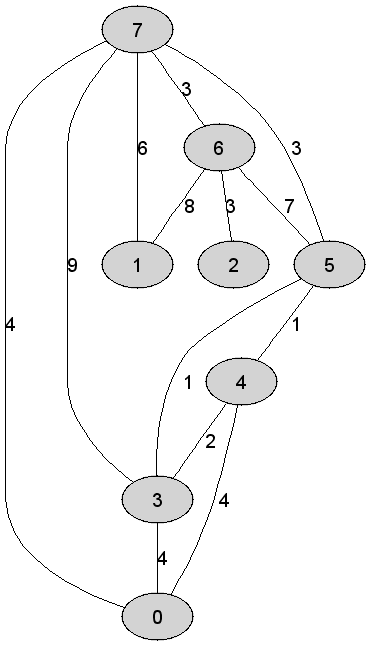
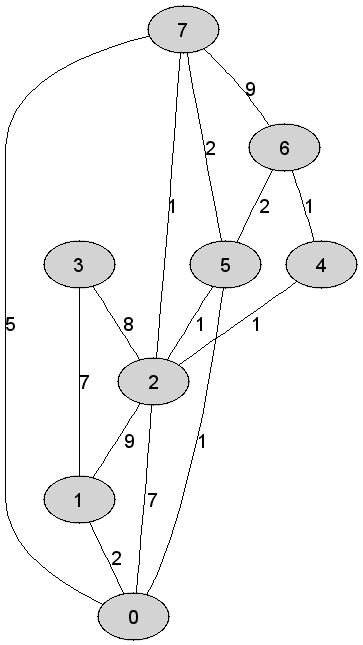
7 |
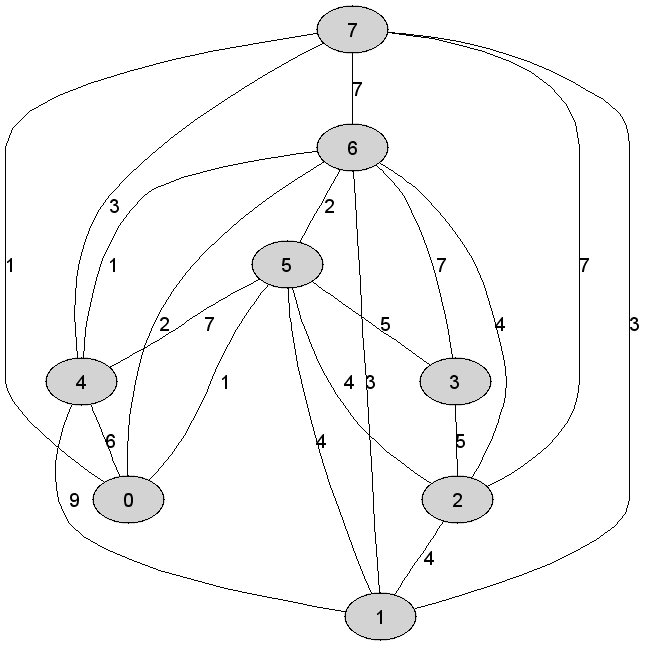
Rozważmy
nieskierowany graf prosty
|
|||
|
Najkrótsza
ścieżka z wierzchołka |
0 |
|||
|
Liczba
wierzchołków wewnętrznych w drzewie najkrótszych ścieżek będącym rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
||
|
Najkrótsza
ścieżka z wierzchołka |
0 |
|||
|
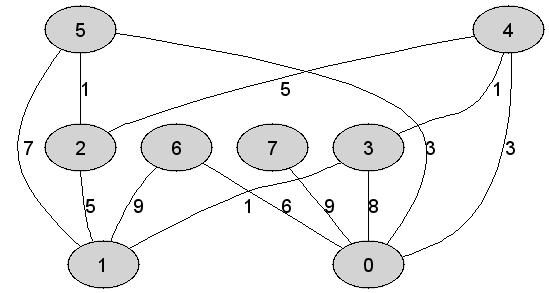
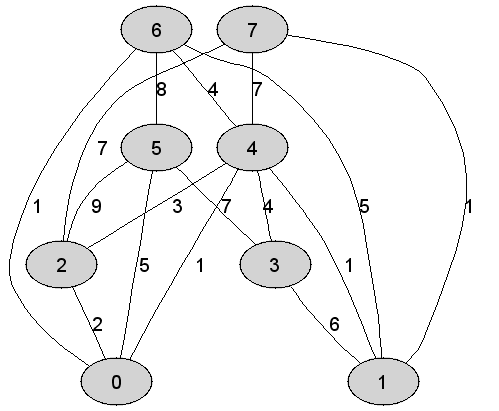
7 |
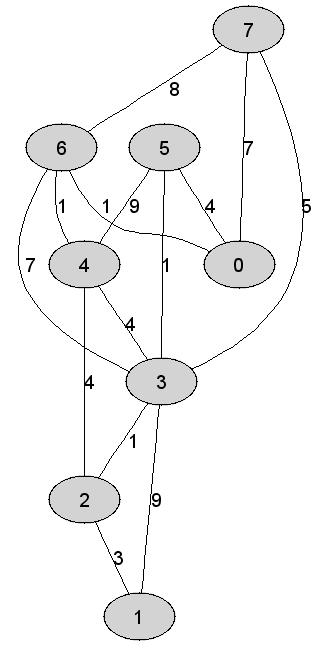
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
0 |
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
1 |
+ |
||
|
Suma wag
krawędzi tworzących drzewo najkrótszych ścieżek będące rezultatem działania
algorytmu Dijkstry jest równa dokładnie |
0 |
|||
|
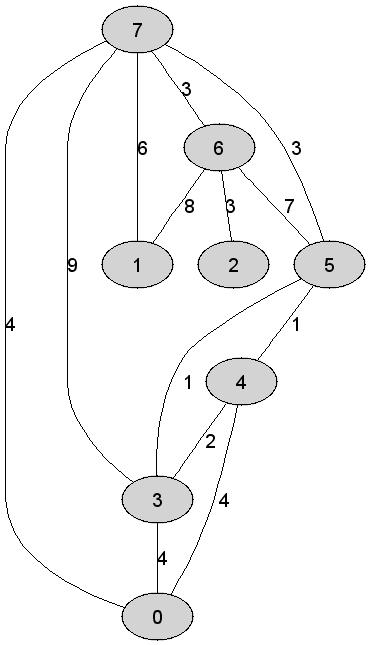
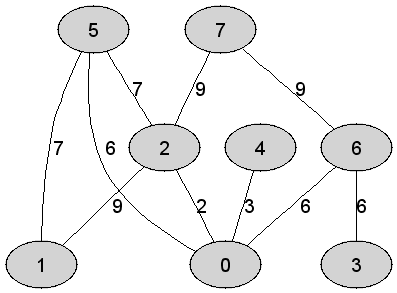
7 |
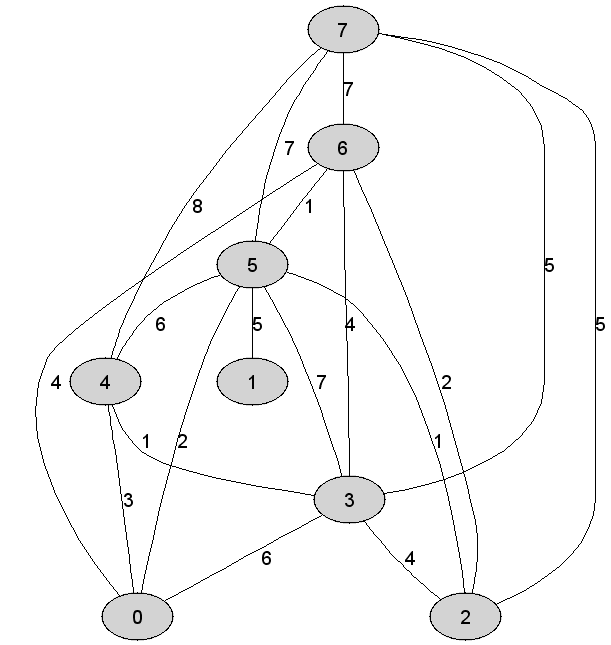
Rozważmy
nieskierowany graf prosty
|
|||
|
Wysokość
drzewa najkrótszych ścieżek będącego rezultatem działania algorytmu Dijkstry
jest równa dokładnie |
1 |
+ |
+ |
|
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
0 |
+ |
||
|
Wierzchołek
|
0 |
+ |
||
|
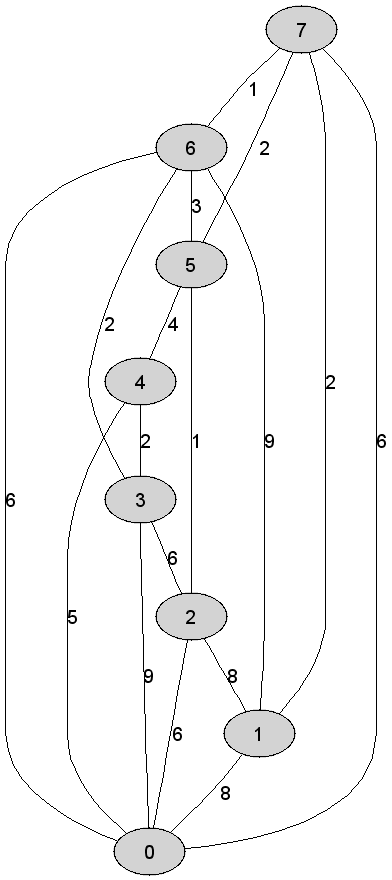
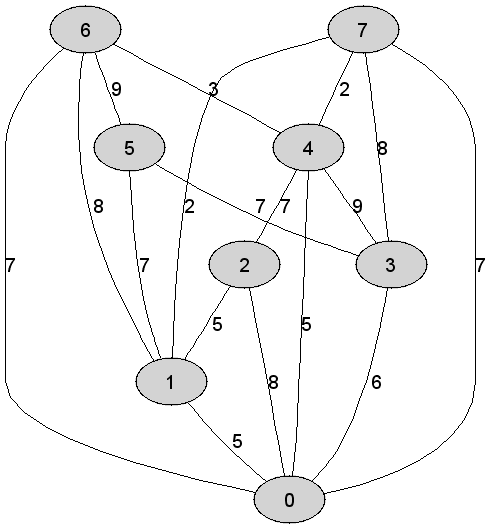
7 |
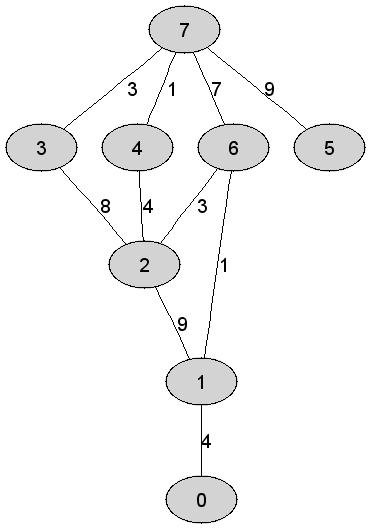
Rozważmy
nieskierowany graf prosty
|
|||
|
Najkrótsza
ścieżka z wierzchołka |
1 |
+ |
||
|
Najkrótsza
ścieżka z wierzchołka |
0 |
+ |
||
|
Wierzchołek
|
0 |
+ |
||
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
|
Liczba wierzchołków zewnętrznych w drzewie
najkrótszych ścieżek będącym rezultatem działania algorytmu Dijkstry jest
równa dokładnie |
0 |
|
|
|
|
Wysokość drzewa najkrótszych ścieżek będącego
rezultatem działania algorytmu Dijkstry jest równa dokładnie |
0 |
|
|
|
|
Wysokość drzewa najkrótszych ścieżek będącego
rezultatem działania algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
|
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków wewnętrznych w drzewie najkrótszych ścieżek będącym rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
||
|
Suma wag
krawędzi tworzących drzewo najkrótszych ścieżek będące rezultatem działania
algorytmu Dijkstry jest równa dokładnie |
0 |
|||
|
Liczba
wierzchołków wewnętrznych w drzewie najkrótszych ścieżek będącym rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
0 |
+ |
||
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków zewnętrznych w drzewie najkrótszych ścieżek będącym rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
1 |
+ |
||
|
Wierzchołek
|
0 |
|||
|
6 |
Rozważmy tablicę |
|||
|
Po pierwszej pętli iteracyjnej (zliczanie) postać tablicy pomocniczej
wykorzystywanej w rozważanym algorytmie jest następująca: |
1 |
+ |
+ |
|
|
Po pierwszej pętli iteracyjnej (zliczanie) postać tablicy pomocniczej
wykorzystywanej w rozważanym algorytmie jest następująca: |
0 |
|||
|
Po trzeciej pętli iteracyjnej (wypisanie) postać tablicy pomocniczej
wykorzystywanej w rozważanym algorytmie jest następująca: |
0 |
|||
|
7 |
Rozważmy nieskierowany graf prosty
|
|||
|
Wysokość drzewa najkrótszych ścieżek będącego rezultatem działania
algorytmu Dijkstry jest równa dokładnie |
0 |
|||
|
Wysokość drzewa najkrótszych ścieżek będącego rezultatem działania
algorytmu Dijkstry jest równa dokładnie |
0 |
|||
|
Suma wag krawędzi tworzących drzewo najkrótszych ścieżek będące rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
+ |
|
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Suma wag
krawędzi tworzących drzewo najkrótszych ścieżek będące rezultatem działania
algorytmu Dijkstry jest równa dokładnie |
0 |
|||
|
Wysokość
drzewa najkrótszych ścieżek będącego rezultatem działania algorytmu Dijkstry
jest równa dokładnie |
1 |
+ |
+ |
|
|
Najkrótsza
ścieżka z wierzchołka |
0 |
|||
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków zewnętrznych w drzewie najkrótszych ścieżek będącym rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
0 |
|||
|
Liczba
wierzchołków zewnętrznych w drzewie najkrótszych ścieżek będącym rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
||
|
Suma wag
krawędzi tworzących drzewo najkrótszych ścieżek będące rezultatem działania
algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
||
|
9 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
0 |
|||
|
Wysokość
drzewa najkrótszych ścieżek będącego rezultatem działania algorytmu Dijkstry
jest równa dokładnie |
0 |
+ |
||
|
Wierzchołek
|
1 |
+ |
||
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
0 |
|||
|
Najkrótsza
ścieżka z wierzchołka |
0 |
|||
|
Najkrótsza
ścieżka z wierzchołka |
1 |
+ |
||
|
9 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
0 |
|||
|
Liczba
wierzchołków zewnętrznych w drzewie najkrótszych ścieżek będącym rezultatem
działania algorytmu Dijkstry jest równa dokładnie |
0 |
|||
|
Najkrótsza
ścieżka z wierzchołka |
1 |
+ |
+ |
|
|
9 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Suma wag
krawędzi tworzących drzewo najkrótszych ścieżek będące rezultatem działania
algorytmu Dijkstry jest równa dokładnie |
1 |
+ |
+ |
|
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
1 |
+ |
+ |
|
|
Wierzchołek
|
0 |
|||
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
0 |
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
0 |
|||
|
Kolejność
przyłączania wierzchołków do drzewa najkrótszych ścieżek grafu |
1 |
+ |
||
|
7 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Wysokość
drzewa najkrótszych ścieżek będącego rezultatem działania algorytmu Dijkstry
jest równa dokładnie |
0 |
+ |
||
|
Wysokość
drzewa najkrótszych ścieżek będącego rezultatem działania algorytmu Dijkstry
jest równa dokładnie |
1 |
+ |
||
|
Najkrótsza
ścieżka z wierzchołka |
0 |
|||