|
18 |
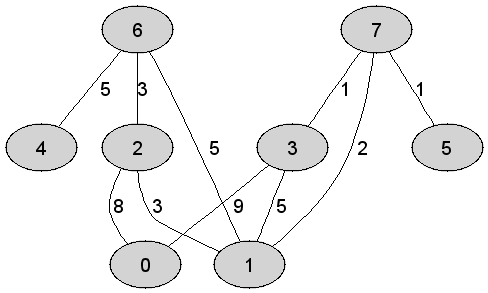
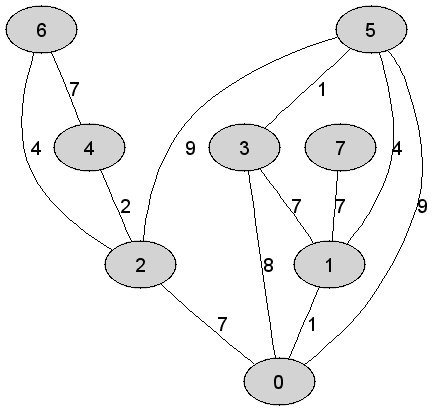
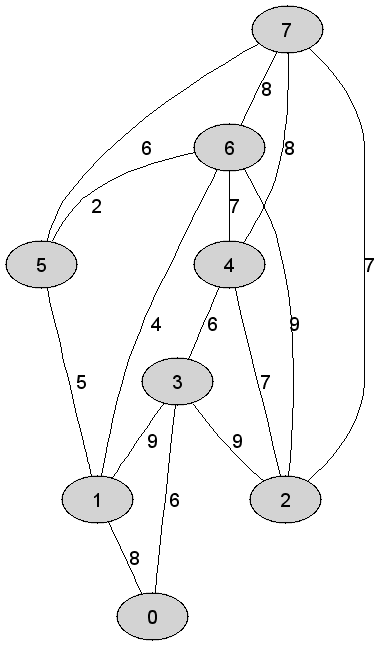
Rozważmy
nieskierowany graf prosty
|
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
1 |
+ |
||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
18 |
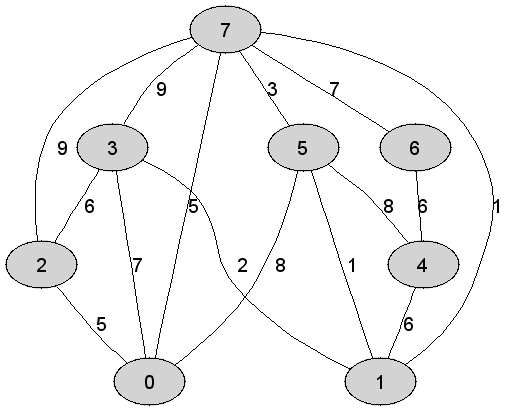
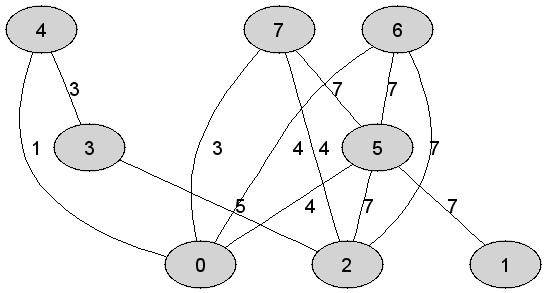
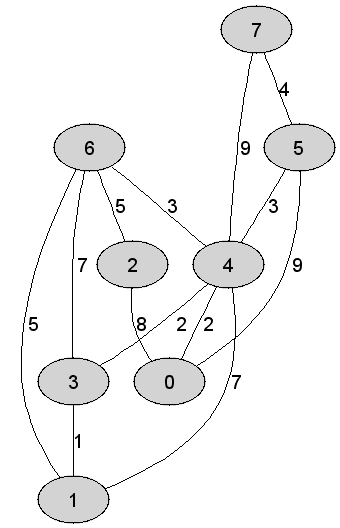
Rozważmy
nieskierowany graf prosty
|
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
Suma wag
krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania
algorytmu Prima jest równa dokładnie |
1 |
+ |
||
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
0 |
|||
|
18 |
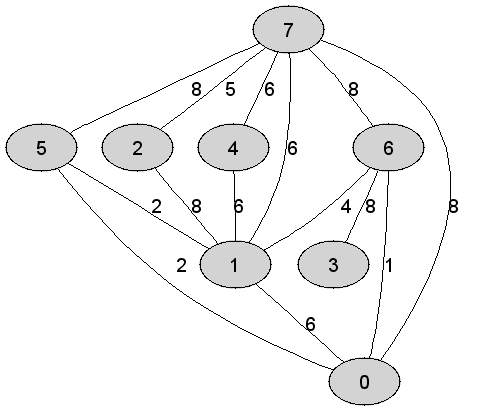
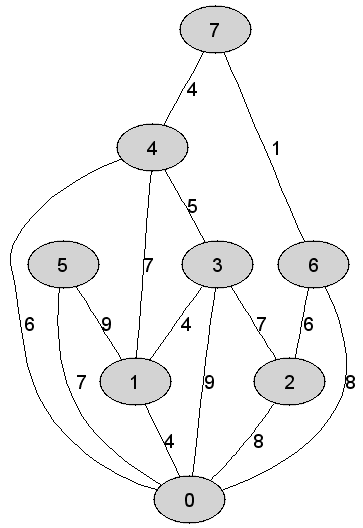
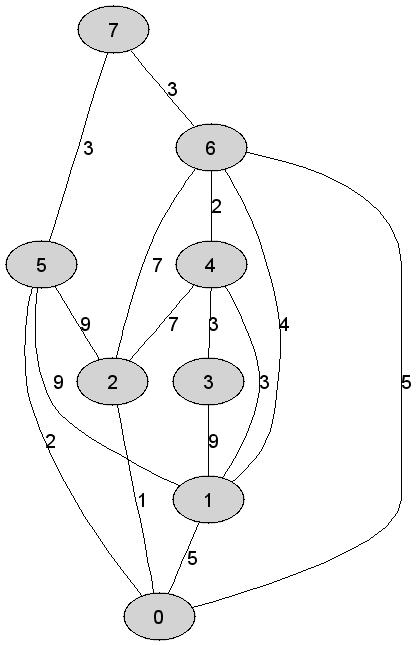
Rozważmy
nieskierowany graf prosty
|
|||
|
Suma wag
krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania
algorytmu Prima jest równa dokładnie |
1 |
+ |
+ |
|
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
+ |
||
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
0 |
+ |
||
|
18 |
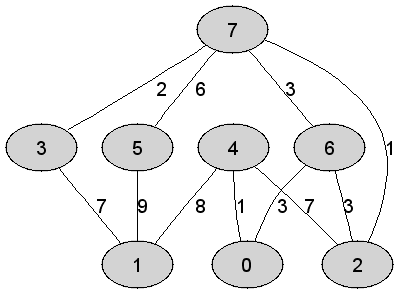
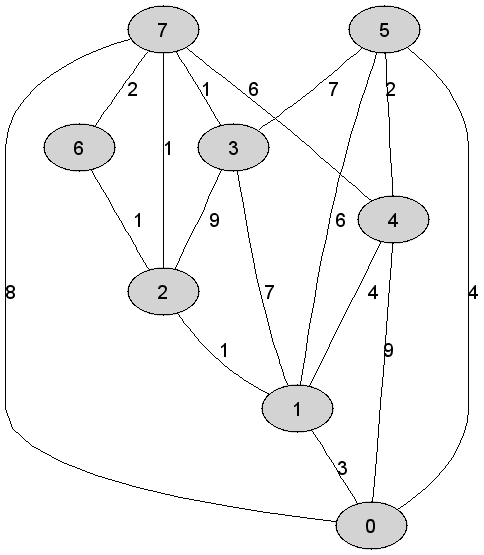
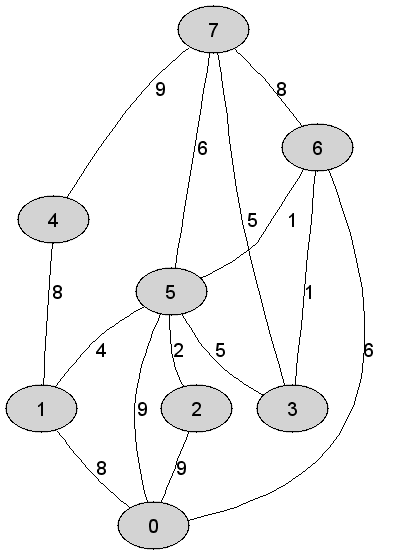
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
1 |
+ |
+ |
|
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
0 |
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
|
Liczba wierzchołków wewnętrznych w minimalym
drzewie rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
|
|
|
Liczba wierzchołków zewnętrznych w minimalym
drzewie rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
|
|
|
Suma wag krawędzi tworzących minimalne drzewo
rozpinające będące rezultatem działania algorytmu Prima jest równa dokładnie |
1 |
+ |
|
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
1 |
+ |
+ |
|
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
0 |
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
1 |
+ |
||
|
18 |
Rozważmy nieskierowany graf prosty
|
|||
|
Kolejność przyłączania wierzchołków do minimalnego drzewa rozpinającego
grafu |
1 |
+ |
+ |
|
|
Suma wag krawędzi tworzących minimalne drzewo rozpinające będące
rezultatem działania algorytmu Prima jest równa dokładnie |
0 |
+ |
||
|
Suma wag krawędzi tworzących minimalne drzewo rozpinające będące
rezultatem działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
Suma wag
krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania
algorytmu Prima jest równa dokładnie |
1 |
+ |
||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
||
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
Liczba
wierzchołków zewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
20 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków zewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
+ |
||
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
0 |
+ |
||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
1 |
+ |
||
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Liczba
wierzchołków zewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
||
|
20 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Kolejność
przyłączania wierzchołków do minimalnego drzewa rozpinającego grafu |
0 |
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
1 |
+ |
+ |
|
|
Liczba
wierzchołków zewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
+ |
|
|
20 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
+ |
||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
||
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Wysokość minimalego drzewa rozpinającego będącego rezultatem
działania algorytmu Prima jest równa dokładnie |
0 |
|||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
1 |
+ |
||
|
Liczba
wierzchołków zewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
18 |
Rozważmy
nieskierowany graf prosty
|
|||
|
Suma wag
krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania
algorytmu Prima jest równa dokładnie |
0 |
+ |
||
|
Liczba
wierzchołków wewnętrznych w minimalym drzewie
rozpinającym będącym rezultatem działania algorytmu Prima jest równa
dokładnie |
0 |
|||
|
Suma wag
krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania
algorytmu Prima jest równa dokładnie |
1 |
+ |
||