1. B-drzewo:
a) jest drzewem zrównoważonym
b)
jest drzewem binarnym
c)
jest drzewem binarnym pełnym
d)
jest drzewem AVL
e)
ma operację sumowania elementów w czasie
* wg niektórych źródeł 'b' w
'b-drzewie' znaczy balanced (zrównoważone). B-drzewo z definicji jest
zrównoważone. Szczególną własnością b-drzewa jest jego szerokość/rozłożystośc.
W b-drzewie każdy wierzchołek poza korzeniem musi mieć n...2n+1 węzłów
potomnych. Wierzchołek drzewa binarnego z definicji ma <= 2 węzły potomne, a
drzewo AVL z definicji jest drzewem binarnym
2. Drzewo AVL:
a) koszt pesymistyczny wyszukiwania
elementu wynosi O(logn)
b) jest drzewem BST
c) jest drzewem binarnym
*Drzewo AVL,
nazywane również drzewem dopuszczalnym,
to zrównoważone binarne drzewo poszukiwań (BST)
Algorytmy podstawowych operacji na drzewie AVL przypominają te z
binarnych drzew poszukiwań, ale są poprzedzane lub następują po nich jedna lub
więcej "rotacji". Wszystkie algorytmy są zazwyczaj realizowane
poprzez rekurencję. Koszt każdej operacji to O(log n).
3. Wstawiamy do
pustego drzewa BST kolejno: 1 0 3 4 6 2 5. Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a)
0 2 5 6 4 3 1
b)
0 2 5 6 4 3 1
c) 0 1 2 3 4 5 6
* inOrder jest zawsze posortowany
4. Wstawiamy do
pustego drzewa BST kolejno: 6 4 3 5 2 0 1. Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a) 1 0 2 3 5 4 6
b) 1 0 2 3 5 4 6
c) 0 1 2 3 4 5 6
* inOrder jest zawsze posortowany
5. Wstawiamy do
pustego drzewa BST kolejno: 0 4 1 2 3 6 5. Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a) 0 1 2 3 4 5 6
b)
3 2 1 5 6 4 0
c)
3 2 1 5 6 4 0
* inOrder jest zawsze posortowany
6. Wstawiamy do
pustego drzewa BST kolejno: 4 0 6 1 3 5 2. Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a)
2 3 1 0 5 6 4
b)
2 3 1 0 5 6 4
c) 0 1 2 3 4 5 6
* inOrder jest zawsze posortowany
7. Wstawiamy do
pustego drzewa BST kolejno: 2 0 6 4 3 1 5.Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a)
1 0 3 5 4 6 2
b)
1 0 3 5 4 6 2
c) 0 1 2 3 4 5 6
* inOrder jest zawsze posortowany
8. Wstawiamy do
pustego drzewa BST kolejno: 2 5 3 6 1 0 4 .Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a) 0 1 2 3 4 5 6
b)
0 1 4 3 6 5 2
c)
0 1 4 3 6 5 2
* inOrder jest zawsze posortowany
9. Wstawiamy do
pustego drzewa BST kolejno: 3 2 5 4 0 6 1 .Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a)
1 0 2 4 6 5 3
b) 0 1 2 3 4 5 6
c)
1 0 2 4 6 5 3
* inOrder jest zawsze posortowany
10. Wstawiamy do
pustego drzewa BST kolejno: 3 0 6 2 4 1 5. Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a)
1 2 0 5 4 6 3
b)
1 2 0 5 4 6 3
c) 0 1 2 3 4 5 6
* inOrder jest zawsze posortowany
11. Wstawiamy do
pustego drzewa BST kolejno: 6 4 5 1 0 2 3. Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a) 0 1 2 3 4 5 6
b)
0 3 2 1 5 4 6
c)
0 3 2 1 5 4 6
* inOrder jest zawsze posortowany
12. Wstawiamy do
pustego drzewa BST kolejno: 5 1 0 3 6 2 4. Wypisując wartości węzłów przy
przejściu drzewa w porządku inorder, otrzymamy:
a) 0 1 2 3 4 5 6
b)
0 2 4 3 1 6 5
c)
0 2 4 3 1 6 5
* inOrder jest zawsze posortowany
13. Wstawiamy do
pustego drzewa BST kolejno: 6 0 5 3 1 4 2. Wypisując wartości węzłów przy
przejściu drzewa w porządku postorder, otrzymamy:
a) 2 1 4 3 5 0 6
b) 2 1 4 3 5 0 6
c)
0 1 2 3 4 5 6
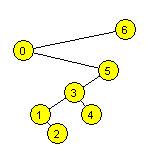
14. Wstawiamy do
pustego drzewa BST kolejno: 2 6 0 3 5 4 1. Wypisując wartości węzłów przy
przejściu drzewa w porządku postorder, otrzymamy:
a) 1 0 4 5 3 6 2
b) 1 0 4 5 3 6 2
c)
0 1 2 3 4 5 6
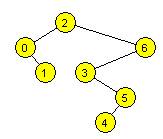
15. Wstawiamy do
pustego drzewa BST kolejno: 1 5 3 2 0 6
4. Wypisując wartości węzłów przy przejściu drzewa w porządku postorder,
otrzymamy:
a) 0 2 4 3 6 5 1
b) 0 2 4 3 6 5 1
c) 0
1 2 3 4 5 6
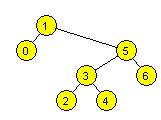
16. Wstawiamy do
pustego drzewa BST kolejno: 3 0 6 2 4 1 5. Wypisując wartości węzłów przy
przejściu tego drzewa w porządku postorder, otrzymamy:
a) 0 1 2 3 4 5 6
b) 1 2 0 5 4 6 3
c) 1 2 0 5 4 6 3
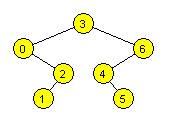
17. Wstawiamy do
pustego drzewa BST kolejno: 2 6 0 3 5 4
1. Wypisując wartości węzłów przy przejściu tego drzewa w porządku
postorder, otrzymamy:
a) 1 0 4 5 3 6 2
b) 1 0 4 5 3 6 2
c) 0 1 2 3 4 5 6
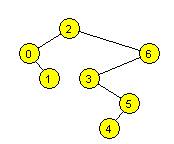
18. Wstawiamy do
pustego drzewa BST kolejno: 1 4 3 2 5 0 6. Wypisując wartości węzłów przy przejściu
drzewa w porządku postorder, otrzymamy:
a) 0 2 3 6 5 4 1
b) 0 2 3 6 5 4 1
c)
0 1 2 3 4 5 6
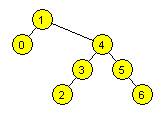
19. Wstawiamy do
pustego drzewa BST kolejno: 1 5 3 2 0 6 4. Wypisując wartości węzłów przy
przejściu drzewa w porządku postorder, otrzymamy:
a) 0 2 4 3 6 5 1
b) 0 2 4 3 6 5 1
c)
0 1 2 3 4 5 6
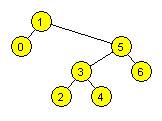
20. Mamy graf niekierowany:
a--b, b--c, c --a. Wykonujemy na nim DFS z punktu ”a” i oznaczamy czasy
rozpoczęcia i zakończenia. Notując x (p/f), gdzie x-wierzchołek, p-czas
rozpoczęcia, f-czas zakończenia przetwarzania, możemy otrzymać:
a)
a(0/5), b(1/3), c(2/4)
b)
a(0/3), b(1/4), c(2/5)
c)
a(0/5), b(1/2), c(3/4)
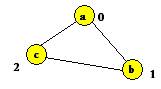
*wg mnie zaczynamy z pkt a przechodzimy przez każdy pkt wiec a=0
b=1 c=2 (odpada odp c)
Jeśli dojdziemy do takiego wierzchołka, że nie ma on krawędzi
incydentych z nieodwiedzonymi wierzchołkami, należy usunąć go ze stosu i pobrać
ze stosu kolejny wierzchołek do przeszukania. Dobra odp: a(0/5), b(1/2), c(3/4)
21. Mamy graf
skierowany złożony z wierzchołków {a,b,c,d} i krawędzi a->b, b->c,
c->d, d->a. Jest on:
a)
drzewem
b)
pełny
c)
acykliczny
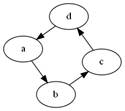
* ma cykl, więc nie jest acykliczny i nie jest drzewem. Na graf
pełny trochę mu brakuje krawędzi
22. Mamy graf
skierowany złożony z wierzchołków {a,b,c,d} i krawędzi a->b, a->c,
b->a, b->c, c->a, c->b. Jest on:
a)
spójny
b)
drzewem
c)
pełny
d)
acykliczny
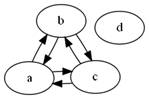
*Graf nazywamy spójnym, jeśli dla każdej pary wierzchołków
istnieje marszruta je łącząca. Zatem nie jest spójny (z powodu wierzchołka D)
Graf pełny jest grafem prostym, w którym dla każdej pary węzłów istnieje
krawędź je łącząca. Zatem nie jest pełny (jw.).
Drzewo to graf spójny bez cykli, więc dany graf również nie jest drzewem
23. Mamy graf
skierowany złożony z wierzchołków {a,b} i krawędzi a->b, b->a. Jest on:
a) pełny
b)
acykliczny
c) spójny
![]()
* jest pełny i spójny, ma cykl
24. Mamy graf
skierowany złożony z wierzchołków {a,b,c,d} i krawędzi a->b. Jest on:
a) acykliczny
b)
spójny
c)
pełny
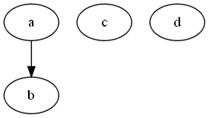
* wszystko jasne J
25. Mamy graf
skierowany złożony z wierzchołków {a} i krawędzi a->a. Jest on:
a)
pełny
b)
acykliczny
c)
drzewem
d) spójny
![]()
* za wiki: Graf pełny jest grafem
prostym, w którym dla każdej pary węzłów istnieje krawędź je łącząca. Graf
prosty - graf bez pętli i krawędzi wielokrotnych. Zatem nie jest grafem
pełnym (ale chyba trzeba jeszcze zajrzeć do wykładu dr Chrzastowskiego)
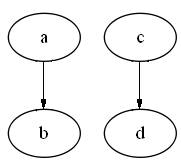
26. Mamy graf
skierowany złożony z wierzchołków {a,b,c,d} i krawędzi a->b, c->d. Jest
on:
a) acykliczny
b)
spójny
c)
pełny
27. Mamy graf
skierowany złożony z wierzchołków {a,b,c,d} i krawędzi a->b, b->a,
c->d, d->c. Jest on:
a)
spójny
b)
drzewem
c)
pełny
d)
acykliczny
* graf jest dwudzielny, więc nie jest
spójny, więc nie jest drzewem i tym bardziej nie jest pełny
28. Listę, ze
zmodyfikowaną operacją get, który przesuwa żądany element na początek listy:
a) warto używać, kiedy większość operacji
get tyczy się małego podzbioru elementów tej listy
b)
warto używać, kiedy większość operacji get tyczy się różnych elementów tej
listy
c) warto używać, kiedy większość operacji
tyczy się jednego elementu
d)
zawsze warto używać, kiedy większość operacji, to operacje get
e)
warto używać dla losowych danych
* szukając na liście elementu, trzeba ją całą przeszukiwać od
początku, zatem im częściej będziemy szukali elementu (grupy elementów)
znajdującego się na początku, tym lepiej dla nas. Wrzucanie wszystkich elementów
na początek nam nic nie da, bo średnio i tak będzie dany element w środku.
29. Listę, ze
zmodyfikowaną operacją get, który przesuwa żądany element na koniec listy:
a)
warto używać, kiedy większość operacji tyczy się jednego elementu
b)
zawsze warto używać, kiedy większość operacji, to operacje get
c) warto używać, kiedy większość operacji
get tyczy się różnych elementów tej listy
d)
warto używać, kiedy większość operacji get tyczy się małego podzbioru elementów
tej listy
e)
warto używać, dla losowych danych
* Jak w przypadku przesuwania na początek, tyle że na odwrót;)
generalnie opłaca się, jesli dzięki temu już nie będziemy musieli przez nie
'przechodzić' przeszukując listę. Dzieje się tak wyłacznie w przypadku, gdy
szukamy różnych elementów
30. Które z niżej
wymienionych wymagają co najmniej O(n) dodatkowej pamięci:
a) CountSort
b) Sortowanie bąbelkowe
c) SelectionSort
*przy okazji merge sort
wymaga O(n) dodatkowej pamięci
31. Porównując
(dla danego algorytmu) złożoność
pesymistyczną pamięciową z oczekiwaną obliczeniową:
a) mogą być sobie równe
b) pierwsza jest (zawsze) nie lepsza od
drugiej
c)
pierwsza jest (zawsze) gorsza od drugiej
* oczywiście mogą być sobie równe (dla
algorytmu np. return null...; tu i tu O(1)), co do drugiego: jest tutaj mały
problem, ja bym raczej tak zaznaczył
32. Porównując
(dla danego algorytmu) złożoność
pesymistyczną pamięciową z oczekiwaną pamięciową:
a)
pierwsza jest (zawsze) gorsza od drugiej
b) pierwsza jest (zawsze) nie lepsza od
drugiej
c)
pierwsza może być lepsza od drugiej
* może być co najwyżej równa
33. Porównując
(dla danego algorytmu) złożoność
pesymistyczną obliczeniową z oczekiwaną pamięciową:
a)
pierwsza jest (zawsze) gorsza od drugiej
b) pierwsza jest (zawsze) nie lepsza od
drugiej
c) mogą być sobie równe
34. Porównując
(dla danego algorytmu) złożoność
pesymistyczną obliczeniową z optymistyczną obliczeniową:
a)
pierwsza może być lepsza od drugiej
b)
pierwsza jest (zawsze)gorsza od drugiej
c) mogą być sobie równe
d) pierwsza jest (zawsze) nie lepsza od
drugiej
* może być co najwyżej równa
35. Porównując
(dla danego algorytmu) złożoność
pesymistyczną obliczeniową z oczekiwaną obliczeniową:
a)
pierwsza jest (zawsze)gorsza od drugiej
b) mogą być sobie równe
c)
pierwsza może być lepsza od drugiej
36. Porównując
(dla danego algorytmu) złożoność oczekiwaną
obliczeniową z oczekiwaną pamięciową:
a)
pierwsza jest (zawsze) gorsza od drugiej
b)
pierwsza jest (zawsze) nie lepsza od drugiej
c) mogą być sobie równe
37. Porównując
(dla danego algorytmu) złożoność oczekiwaną
obliczeniową z optymistyczną pamięciową:
a) mogą być sobie równe
b) pierwsza jest (zawsze) nie lepsza od
drugiej
c)
pierwsza jest (zawsze) gorsza od drugiej
38. Szybkiej transformaty
Fouriera używamy do:
a) analizy i obróbki sygnałów dźwiękowych
b)
znajdowania najkrótszej ścieżki w grafie
c) mnożenia wielomianów
d) mnożenia liczb
e)
sortowania
39. Jakie jest
najlepsze oszacowanie na złożoność problemu znajdowania największego elementu w
posortowanej tablicy rozmiaru n:
a)
O(n)
b)
O(lgn)
c) O(1)
w zależności czy rosnąco czy malejąco
posortowana jest tablica, element ten znajduje się pod pierwszym lub ostatnim
indeksem
40. Jakie jest
najlepsze oszacowanie na złożoność problemu znajdowania największego elementu w
danej tablicy rozmiaru n:
a) O(n)
b)
O(lgn)
c)
O(1)
41. Mnożenie
dwóch n-cyfrowych liczb da się wykonać w czasie:
a)
O(nlogn)
b)
O(n2)
c)
O(nlog23))
d)
O(n)
*odpowiednio algorytmy: FFT, 'pod
kreską', Karatsuby
42. Dla
posortowanej niemalejąco tablicy A następujący algorytm:
I=0;
p=n-1;
while(I<p){
s=(I+p+1)/2;
if(x<A[s])
p=s-1;
else
I=s;
}
return I:
a) oblicza indeks ostatniego wystąpienia
największej liczby nieprzekraczającej x
b)
oblicza indeks ostatniego wystąpienia najmniejszej liczby nieprzekraczającej x
c)
oblicza indeks pierwszego wystąpienia najmniejszej liczby co najmniej równej x
d)
oblicza indeks ostatniego wystąpienia x w A
e)
oblicza indeks pierwszego wystąpienia x w A
f)
oblicza indeks pierwszego wystąpienia największej liczby nieprzekraczającej x
g) zawsze działa w czasie O(logn)
h)
może się zapętlić
43. Algorytm
Karacuby służy do:
a)
analizy i obróbki sygnałów dźwiękowych
b)
przechodzenia grafu
c)
znajdowania najkrótszej ścieżki w grafie
d)
sortowania
e) mnożenia wielomianów
f) mnożenia liczb
44. Stabilne są
algorytmy sortowania:
a) Insertionsort
b) Selectionsort
c) MergeSort
d) HeapSort
e) QuickSort
45. Spośród następujących
rzędów złożoności minimalne są:
a) O(2log n)
b)
O(n log n)
c) O(ln 2n)
* O(2logn) = O(n) <
O(nlogn)
O(ln2n) = O(nln2) = O(n) < O(nlogn)
46. Spośród
następujących rzędów złożoności minimalne są:
a) O(ln 2n)
b) O(log102n)
c)
O(nlogn)
* O(ln2n) = O(nln2) = O(n)
< O(nlogn)
O(log102n) = O(nlog102) = O(n) < O(nlogn)
47. Algorytm
Bluma-Floyda-Pratta-Rivesta-Tarjana znajdowania k-tego co do wielkości elementu
w n-elementowym zbiorze zaczyna się od podziału na m-elementowe podzbiory dla
m=5. Gdyby analogicznie pomysł wykorzystać dla innej, ale ustalonej z góry
liczności m, to liniową złożoność pesymistyczną uzyskalibyśmy dla:
a) m=3
b)
m=n/5
c) m=7
d)
m=√(n)
* algorytm 'magicznych piątek' rzeczywiście działa najlepiej dla
m=5, jednak dla stałych m nie będących 'dostatecznie bliskimi n' i nie
mniejszymi od 5 wciąż działa liniowo
48. Jeżeli
pewien algorytm działa w pesymistycznym
czasie O(n) dla danych wielkości n, to będzie działał w pesymistycznym czasie
O(n) również dla danych wielkości:
a) n+1
b) 2n
c) 2n + 2ln n
d) logn
e) nlogn
f) 2n + 2ln n
g)
n2
49. Jeżeli
pewien algorytm działa w pesymistycznym
czasie O(nlogn) dla danych wielkości n, to będzie działał w pesymistycznym
czasie O(nlogn) również dla danych wielkości:
a) n+1
b) 2n + 2ln n
c) nlogn
d) 2n
e) n2
f) logn
50. Jeżeli
pewien algorytm działa w pesymistycznym czasie O(logn) dla danych wielkości n,
to będzie działał w pesymistycznym czasie O(logn) również dla danych wielkości:
a) 2n
b) logn
c) n2
51. Rozważmy
graf pełny z wagami G=(V,E), gdzie |V| =n, wtedy:
a) rozmiar tablicy list incydencji grafu G
jest rzędu Θ(n2)
b rozmiar macierzy sąsiedztwa grafu G jest
rzędu Θ(n2)
c)
rozmiar macierzy sąsiedztwa grafu G jest rzędu Θ(n)
d) rozmiar tablicy list incydencji grafu G
jest rzędu Ω(n)
e) rozmiar tablicy list incydencji grafu G
jest rzędu Ω(n)
52. Rozważmy algorytm
sortowania przez zliczenie CS zastosowany do sortowania n-elementowego ciągu
binarnego X, wtedy:
a)
w tym przypadku rezultatem działania algorytmu CS będzie ciąg binarny
uporządkowany nierosnąco
b)
S(CS(X),n)= Θ(n2)
c) T(CS(X),n,m)=Œ(n+m), gdzie m jest
stałą nie większą niż 4
d) A(CS(X),n)≠W(CS(X),n)
e) S(CS(X),n)= Θ(n)
* ad1: sortujemy rosnąco raczej;),
ad2: S(CS(X),n)=O(n+m), a m=2, więc tutaj złożoność pamięciowa to O(n), ad3:
ponieważ T(CS(X),n,m)=Θ(n+m), więc czy tam jest theta, czy omega, czy duże
o - nie robi róznicy, ad4: countSort chyba nie miał gorszych i lepszych dni
(nie sortuje przez porównania)
53. Rozważmy
algorytm sortowania przez wstawianie IS, z binarnym wyszukiwaniem pozycji dla
wstawianego elementu, zastosowany do
danych wejściowych rozmiaru n, wtedy:
a) W(IS,n)=O(n×lg(n)), jeżeli operacją
dominującą jest przestawianie danych
b) W(IS,n)=Ω(A(IS,n)), jeżeli operacją
dominującą jest porównywanie danych
c) W(IS,n)= Θ (A(IS,n)), jeżeli
operacją dominującą jest przestawianie danych
d)
W(IS,n)= Θ(n2), jeżeli operacją dominującą jest przestawianie
danych
e)
W(IS,n)=O(n×lg(n)), jeżeli operacją dominującą jest porównywanie danych
54. Rozważmy zastosowanie
algorytmu sortowania przez scalanie MS do uporządkowanych nierosnąco danych
wejściowych X rozmiaru n, wtedy:
a) T(MS(X),n)= Θ(lg(n!))
b)
w tym przypadku wysokość drzewa wywołań rekurencyjnych algorytmu MS będzie nie
mniejsza niż n
c)
T(MS(X),n)= O(n)
55. Rozważmy
algorytm HeapSort zastosowany do sortowania n-elementowego ciągu wejściowego
zapisanego w tablicy X, wtedy:
a)
W(HeapSort(X),n)=O(n), jeżeli operacją dominującą jest czynność przedstawiania
elementów tablicy
b) algorytm HeapSort sortuje dane wejściowe
w miejscu
c)
w drzewie decyzyjnego algorytmu HeapSort zastosowanego do rozważanych danych
może istnieć ścieżka korzeń-liść, której
długość jest rzędu O(n)
d) S(HeapSort(X),n)=O(1)
* ad1: na oko jest to O(n2),
ad2: wersja z daną tablicą sortuje już na niej; nie potrzebujemy
dodatkowej; ad3: wtf is decyzyjny alg. heapsort? w każdym razie drzewka
decyzyjne lubią być pełnymi drzewami binarnymi wysokości co najmniej lg(n!),
ad4: to znaczy, że sortuje w miejscu
56. Niech Alg
będzie optymalnym algorytmem dla problemu wyszukania pewnego
elementu(zakładamy, że takowy istnieje) w n-elementowym nieuporządkowanym
uniwersum, wtedy:
a)
A(Alg, n)= Ω(nxlg(n))
b)
W(Alg, n)=O(n1/2)
c) A(Alg, n)=O(W(Alg,n))
* żeby znaleźć jakikolwiek element musimy wykonać co najwyżej
O(n) porównań, średnio n/2
57. Rozważmy
graf pełny G=(V,E), gdzie V=a,b,c,d,e,f,g wtedy:
a) koszt algorytmu BFS dla rozważanego
grafu G jest rzędu O(|V|+|E|)
b)
kolejność odwiedzania wierzchołków grafu G z wierzchołka startowego d przez
algorytm BFS jest następująca: d,c,e,b,f,a,g,
jeżeli wierzchołki wybieramy w porządku
odwrotnym do alfabetycznego
c) kolejność odwiedzania wierzchołków grafu
G z wierzchołka startowego d przez algorytm BFS jest następująca: d,g,f,e,c,b,a,
jeżeli wierzchołki wybieramy w porządku
odwrotnym do alfabetycznego
d)
kolejność odwiedzania wierzchołków grafu G z wierzchołka startowego d przez
algorytm BFS jest następująca: d,a,b,c,e,f,g,
jeżeli
wierzchołki wybieramy w porządku alfabetycznym
e)
koszt algorytmu BFS dla rozważanego grafu G jest rzędu Θ(|V|)
f)
koszt algorytmu DFS dla rozważanego grafu G jest rzędu O(|V|)
g)
kolejność odwiedzania wierzchołków grafu G z wierzchołka startowego d przez
algorytm DFS jest następująca: d,a,g,b,f,c,e
jeżeli
wierzchołki wybieramy w porządku alfabetycznym
h) kolejność odwiedzania wierzchołków grafu
G z wierzchołka startowego d przez algorytm DFS jest następująca: d,a,b,c,e,f,g
jeżeli
wierzchołki wybieramy w porządku alfabetycznym
* ad1: bfs ma taki koszt dla każdego
grafu
ad3: bfs(breadth-first-search), czyli algorytm przeszukiwania wszerz szuka
'płytko' - poziomami. Ponieważ jest to graf pełny, to z wierzchołka d po prostu
po kolei odwiedzi wszystkie wierzchołki w kolejności odwrotnej do alfabetycznej
ad5/6: koszt dfs i bfs to Θ(|V|+|E|)
ad7: dfs(depth-first-search), czyli algorytm przeszukiwania wgłąb szuka
'głęboko' (generalnie znajdzie najdłuższą drogą od wierzchołka początkowego).
Ponieważ graf jest pełny to znajdzie najdłuższą drogę - składająca się ze
wszystkich wierzchołków odwiedzanych zgodnie z kolejnością alfabetyczną
58. Rozważmy
graf G=(V,E), gdzie |V|=n i n>10, w
którym algorytmy DFS oraz BFS generują ten sam ciąg etykiet odwiedzanych
wierzchołków z pewnego wierzchołka źródłowego, wtedy graf G może być:
a)
grafem-drzewem binarnym wysokości Θ(lg(n))
b) grafem pustym
c) grafem-gwiazdą, tj. grafem spójnym
takim, że każdy wierzchołek tego grafu ma rząd równy 1 za wyjątkiem wierzchołka
centralnego, którego rząd jest
równy n-1
d) grafem-drzewem binarnym wysokości n-1
* w przypadku grafu pustego DFS i BFS
dadzą w wyniku listę pustą, grafu-drzewa wysokości n-1 (czyli de facto listy)
wypiszą po kolei elementy listy, w przypadku gwiazdy jest to prawdziwe, jeśli
zaczynamy od wierzchołka centralnego
59. Niech H
będzie kopcem-drzewem typu min powstałym przez kolejne wstawianie wierzchołków
o etykietach 8,2,4,7,6,1,3,0,5 do początkowo pustej struktury, wtedy:
a) wierzchołki kopca-drzewa H wypisane w
kolejności PreOrder tworzą ciąg: 0,1,5,8,6,7,2,4,3
b) wierzchołki kopca-drzewa H wypisane w
kolejności InOrder tworzą ciąg: 8,5,6,1,7,0,4,2,3
c) wysokość kopca-drzewa H jest rzędu
lg(n), gdzie n jest liczbą wierzchołków rozważanego drzewa
d) wysokość kopca-drzewa H jest równa 3
e) jeżeli w kopcu-drzewie H wykonamy
operację delmin, to etykiety kopca-drzewa będącego rezultatem rozważanej
operacji
sczytane
w kolejności InOrder tworzą ciąg 1,2,3,4,5,6,7,8
f) jeżeli w kopcu-drzewie H wykonamy
operację delmin, to etykiety kopca-drzewa będącego rezultatem rozważanej
operacji
sczytane
w kolejności PostOrder tworzą ciąg 8,6,7,5,4,3,2,1
g) liczba liści na ostatnim poziomie
kopca-drzewa H jest równa 2
h)
jeżeli w kopcu-drzewie H wykonamy operację delmin, to etykiety kopca-drzewa
będącego rezultatem rozważanej operacji
sczytane w kolejności PreOrder tworzą
1,2,5,6,7,4,3,8
i) wysokość kopca-drzewa H jest niezależna
od kolejności wstawiania rozważanych wierzchołków
*by s5578: (nie biorę za to
najmniejszej odpowiedzialności;)
Ad3.Wysokość węzła definiujemy jako liczbę krawędzi na najdłuższej prostej
ścieżce prowadzącej od tego węzła do liścia, wysokość drzewa jest więc
wysokością korzenia. Jak łatwo zauważyc, wysokość kopca zawierającego n węzłów
(wierzchołków) wynosi (lg n)
Ad5.kolejność inOrder 86571423
Ad8.kolejność preOrder 15687243
by s5413:
// z liczenia i rysowania, nie gwarantuje poprawności
+ a) wierzchołki kopca-drzewa H wypisane w kolejności PreOrder tworzą ciąg:
0,1,5,8,6,7,2,4,3
+ b) wierzchołki kopca-drzewa H wypisane w kolejności InOrder tworzą ciąg:
8,5,6,1,7,0,4,2,3 // wbrew pozorom, to nie jest BST, więc nie da ciągu
posortowanego
+ c) wysokość kopca-drzewa H jest rzędu lg(n), gdzie n jest liczbą wierzchołków
rozważanego drzewa
- d) wysokość kopca-drzewa H jest równa 3 // 4 jakby liczyć korzeń
+ e) jeżeli w kopcu-drzewie H wykonamy operację delmin, to etykiety
kopca-drzewa będącego rezultatem rozważanej operacji sczytane w kolejności
InOrder tworzą ciąg 1,2,3,4,5,6,7,8
+ f) jeżeli w kopcu-drzewie H wykonamy operację delmin, to etykiety
kopca-drzewa będącego rezultatem rozważanej operacji sczytane w kolejności
PostOrder tworzą ciąg 8,6,7,5,4,3,2,1
+ g) liczba liści na ostatnim poziomie kopca-drzewa H jest równa 2
- h) jeżeli w kopcu-drzewie H wykonamy operację delmin, to etykiety
kopca-drzewa będącego rezultatem rozważanej operacji sczytane w kolejności
PreOrder tworzą 1,2,5,6,7,4,3,8
+ i) wysokość kopca-drzewa H jest niezależna od kolejności wstawiania
rozważanych wierzchołków
60. Niech D
będzie drzewem decyzyjnym dla pewnego algorytmu sortowania przez porównania
zastosowanego do danych wejściowych rozmiaru n, wtedy:
a)
liczba liści w drzewie D jest co najwyżej rzędu n2
b) liczba liści w drzewie D jest co
najmniej rzędu nn
c)
wysokość drzewa D jest rzędu co najwyżej lg(n!)
d) wysokość drzewa D jest rzędu co najmniej
lg(n!)
61. Niech T
będzie drzewem BST powstałym przez losowe
wstawianie wierzchołków o etykietach 8,2,4,7,6,1,3,0,5 do początkowo pustej
struktury, wtedy:
a)
wierzchołki drzewa T wypisane w kolejności InOrder tworzą ciąg nierosnący
b) wierzchołki drzewa T wypisane w
kolejności InOrder mogą odpowiadać ciągowi wierzchołków w kolejności PostOrder
c)
wysokość drzewa T jest równa co najwyżej 5
d) wysokość drzewa T jest zależna od
kolejności wstawiania rozważanych wierzchołków i w przypadku pesymistycznym
może
być równa 8
e) wysokość drzewa T jest równa co najmniej
lg(n), gdzie n jest liczbą wierzchołków rozważanego drzewa
* ad2 dla drzewa listy bez prawego
poddrzewa, ad4 jeśli drzewo jest listą, ad5 wysokośc drzewa idealnie
zbalansowanego wynosi lg(n), więc każde drzewo musi być co najmniej tej
wysokości
62. Niech T
będzie drzewem BST powstałym przez kolejne
wstawianie wierzchołków o etykietach 8,2,4,7,6,1,3,0,5 do początkowo pustej
struktury, wtedy:
a)
wysokość drzewa T jest równa co najwyżej lg(n), gdzie n jest liczbą
wierzchołków rozważanego drzewa
b)
wierzchołki drzewa T wypisane w kolejności InOrder tworzą ciąg
8,0,1,2,3,4,7,5,6
c) usunięcie wierzchołka z etykietą 8 w
drzewie T prowadzi do drzewa, którego korzeniem będzie wierzchołek z etykietą 2
d) usunięcie wierzchołka z etykietą 2 w
drzewie T prowadzi do drzewa, w którym w miejscu wierzchołka z etykietą 2
znajdzie
się wierzchołek z etykietą 1 lub 3
e)
usunięcie wierzchołka z etykietą 2 w drzewie T prowadzi do drzewa, w którym w
miejscu wierzchołka z etykietą 2 znajdzie
się wierzchołek z etykietą 4
63. Załóżmy, że
kolejka Q zawiera n elementów i że wykonujemy jedynie operacje zdefiniowane w
strukturze kolejek, wtedy:
a)
wycięcie z kolejki Q elementu znajdującego się w odległości n/4 względem
początku kolejki wymaga wcześniejszego
wyjęcia z kolejki 3n/4±1 elementów
b)
wycięcie z kolejki Q elementu znajdującego się w odległości n względem końca
kolejki wymaga wcześniejszego wyjęcia z
kolejki n±1 elementów
c) wycięcie z kolejki Q elementu
znajdującego się w odległości n/4 względem początku kolejki wymaga
wcześniejszego
wyjęcia z kolejki n/4±1 elementów
d)
wycięcie z kolejki Q elementu znajdującego się w odległości 1 względem początku
kolejki wymaga wcześniejszego wyjęcia
z kolejki n±1 elementów
e) używając tylko co najwyżej dwóch kolejek
pomocniczych Q1 oraz Q2 i operacji kolejkowych można odwrócić kolejność
elementów w kolejce Q
64. Załóżmy, że stos
S zawiera n elementów i że wykonujemy jedynie operacje zdefiniowane w
strukturze stosów, wtedy:
a) zdjęcie ze stosu S elementu znajdującego
się na wysokości n/4 względem góry stosu wymaga wcześniejszego zdjęcia ze
stosu
n/4±1 elementów
b) zdjęcie ze stosu S elementu znajdującego
się na wysokości n względem góry stosu wymaga wcześniejszego zdjęcia ze stosu
n±1 elementów
c) używając tylko co najwyżej dwóch stosów
pomocniczych S1 i S2 i operacji stosowanych można odwrócić kolejność
elementów na stosie S
d)
zdjęcie ze stosu S elementu znajdującego się na wysokości 1 względem góry stosu
wymaga wcześniejszego zdjęcia ze stosu
n±1 elementów
65. Nazwa
struktury danych AVL i związany z nią algorytm pochodzi od:
a)
pierwszych liter nazwisk trzech twórców tej metody
b)
pierwszych liter angielskiego skrótu opisującego najważniejszą cechę tej
struktury
c)
nazwy uniwersyteckiej ligi siatkówki, której pasjonatami byli jej twórcy
* avl pochodzi od liter nazwisk dwóch
twórców (Adelson-Velsky i Landis). Jeden z żartów dr Chrząstowskiego to właśnie
'trzech twórców AVL: Adelson, Velsky i Landis';), co ciekawe p. Rembelski w
wykładach ma 3 twórców ;)
66. Niech T
będzie drzewem AVL powstałym przez kolejne wstawianie wierzchołków o etykietach
8,2,4,7,6,1,3,0,5 do początkowo pustej struktury, wtedy:
a)
wysokość drzewa jest równa 4
b)
w trakcie budowy drzewa wykonamy co najmniej dwie podwójne rotacje
c) w trakcie budowy
drzewa T wykonamy dwie podwójne i jedną pojedynczą rotację
d) wysokość drzewa
jest niezależna od kolejności wstawiania rozważanych wierzchołków
e)
wierzchołki
drzewa ![]() wypisane
w kolejności PreOrder tworzą ciąg 3,4,2,1,0,7,6,5,8
wypisane
w kolejności PreOrder tworzą ciąg 3,4,2,1,0,7,6,5,8
f)
wierzchołki
drzewa ![]() wypisane
w kolejności PostOrder tworzą ciąg 0,1,3,2,5,6,8,7,4
wypisane
w kolejności PostOrder tworzą ciąg 0,1,3,2,5,6,8,7,4
g) wierzchołki
drzewa ![]() wypisane
w kolejności InOrder tworzą ciąg 0,1,2,3,4,5,6,7,8
wypisane
w kolejności InOrder tworzą ciąg 0,1,2,3,4,5,6,7,8
wysokość drzewa jest równa 3.
Kolejność PreOrder 421036578
Kolejność PostOrder 013258764
Kolejność InOrder 012345678
67. Kopiec
n-elementowy można:
a)
przekształcić w kopiec odwrotny(z najmniejszym, a nie największym elementem w
każdym korzeniu) w czasie O(n)
b)
rozebrać w czasie O(n)
c) utworzyć w czasie O(n)
d) scalić z innym kopcem n-elementowym
(czyli utworzyć nowy kopiec z tych dwóch) w czasie O(n)
*ad1/2 przekształcenie w kopiec
odwrotny wymusza rozebranie kopca. Czy da się to zrobić liniowo? Generalnie
patrząc na operacje dozwolone na kopcu, to musimy po prostu rozebrać go jak
przy heapSorcie, jednakże można to też zrobić jakimś algorytmem dobierającym
się do wierzchołków metodą bottom-up (czyli np. postOrder) i po kolei dodawać
wierzchołki do nowoutworzonego kopca typu max (co jest liniowe) tworząc go
liniowo heapConstructem. Jak jest w kluczu? Może ktoś wie?:)
ad3: heapConstruct
68. Które z
poniższych zdań jest zawsze prawdziwe w strukturze kolejek priorytetowych typu
min: NIEopracowane
a) empty(pq)→empty(delmin(insert(insert(pq,e),e)))
b) min(pq)=min(insert(delmin(pq),min(pq)))
c) min(pq)=min(insert(pq,e))
d) empty(pq)→empty(delmin(insert(pq,e),e))
*ad1: kolejka priorytetowa w
standardowej wersji ma cechy multizbioru (elementy mogą się powtarzać), więc po
dwukrotnym wstawieniu i jednokrotnym usunięciu zostaje jeszcze jeden element
ad2: wg p. Rembelskiego - czemu? nie wiem... Może dlatego, że nie chodzi o
wartość minimalną, a element minimalny. O ile wartości minimalne są te same, to
elementy różne...
ad3: e może być nowym elementem minimalnym
69. Które z
poniższych zdań jest zawsze prawdziwe w strukturze kolejek:
a) ¬empty(q) → empty(out(q))=true
b) ¬empty(q) →first(q)≠first(in(out(q),e))
c) out(in(in(q,e),e))=in(out(in(q,e)),e)
70. Niech X=[0,3,2,4,3,3,2,0,0]
będzie tablicą danych wejściowych dla algorytmu sortowania przez zliczenie CS,
wtedy:
a)
stan tablicy pomocniczej, w której odbywa się zliczanie, po zakończeniu
sumowania(tj. tuż po 3-ciej pętli iteracyjnej
algorytmu CS) jest następujący [3,3,5,7,9]
b)
stan tablicy pomocniczej, w której odbywa się zliczanie, po zakończeniu
sumowania(tj. tuż po 3-ciej pętli iteracyjnej
algorytmu CS) jest następujący [2,3,5,8,9]
c) rozmiar tablicy pomocniczej niezbędnej
do realizacji czynności zliczania w algorytmie CS jest nie mniejszy niż 5
d) stan tablicy pomocniczej, w której
odbywa się zliczanie, po zakończeniu sumowania(tj. tuż po 2-giej pętli
iteracyjnej
algorytmu
CS) jest następujący [3,0,2,3,1]
*tablica pomocnicza po zakończeniu
sumowania wygląda tak [3,3,5,8,9]
71. Które z
poniższych zdań jest prawdziwe: NIEopracowane
a)
istnieje algorytm, który z zadanego n-wierzchołkowego kopca-drzewa konstruuje
drzewo BST w czasie O(n)
b)
istnieje algorytm, który konstruuje kopiec-drzewo z losowego ciągu n elementów
wejściowych w czasie O(n)
c)
istnieje algorytm, który z zadanego n-wierzchołkowego drzewa AVL konstruuje
kopiec-drzewo w czasie O(n1/2)
d)
istnieje algorytm, który konstruuje kopiec-drzewo z losowego ciągu n elementów
wejściowych w czasie O(lg(n))
e)
istnieje algorytm, który z zadanego n-wierzchołkowego kopca-drzewa konstruuje
drzewo AVL w czasie O(n× lg(n))
72. Rozważmy
algorytm Alg i korzeń drzewa binarnego root, gdzie Alg(root)=
{
if(root==NULL)
return
0
else
if(root.left==NULL AND root.right==NULL)
return
1
else
return Alg(root.left) + Alg(root.right) +1
},
wtedy:
a)
rezultatem wywołania algorytmu Alg dla drzewa binarnego o korzeniu root jest
liczba wierzchołków zewnętrznych tego drzewa
b)
rezultatem wywołania algorytmu
Alg dla drzewa binarnego o korzeniu root jest liczba wierzchołków tego drzewa
c)
rezultatem wywołania algorytmu Alg dla drzewa binarnego o korzeniu root jest liczba
wierzchołków wewnętrzn. tego drzewa
d)
S(Alg, root)=Θ(n), gdzie
n jest liczbą wierzchołków drzewa o korzeniu root i uwzględniamy stos wywołań
rekurencyjnych
e)
rezultatem wywołania algorytmu Alg dla drzewa binarnego o korzeniu root jest
wysokość tego drzewa
73. Rozważmy
algorytm Alg(n)=
{
int k=1, x=1;
while(k<n)
do
k=k+1;
x=x*k
od
}.
Która z wymienionych poniżej formuł jest
niezmiennikiem pętli iteracyjnej w algorytmie Alg?
a)
x=1+2+3+…+(k-1)+k
b)
x=x*k i k ≤x
c)
x=k!
d) x=k! i x≥k
e)
x=k! i s≥k
f)
k ≤n
* jeśli mamy zaznaczyć tylko jedno
74. Rozważmy
algorytm Alg(n)=
{
int s=0, k=1;
while(k<=n) do
s=k*k;
k=k+1
od
}.
Które z poniższych zdań jest prawdziwe:
a) algorytm Alg zatrzymuje się dla dowolnej
parzystej liczby naturalnej
b)
algorytm Alg jest całkowicie poprawny dla warunku początkowego i końcowego
odpowiednio WP=(n jest liczbą naturalną)
oraz WK=(s=Σni=1 (i+k2))
c)
algorytm Alg nie zatrzymuje się dla dowolnej liczby naturalnej n≥210
75. Rozważmy
algorytm Alg(n)=
{
int s=0, k=1;
while(k<=n) do
s=s+k*k;
k=k+1
od
}.
Które z poniższych zdań jest prawdziwe:
a)
Algorytm Alg jest całkowicie poprawny dla warunku początkowego i końcowego
odpowiednio WP=(n jest liczbą naturalną)
oraz WK=(s=Σni=1(i-1)2)
b)
Algorytm Alg jest całkowicie poprawny dla warunku początkowego i końcowego
odpowiednio WP=(n jest liczbą naturalną)
oraz WK=(s=Σni=1(i+k)2)
c) Algorytm Alg jest częściowo poprawny dla
warunku początkowego i końcowego odpowiednio WP=(n jest liczbą naturalną)
oraz WK=(s=Σni=1 i2)
76. Rozważmy
algorytm Alg(n)=
{
if(n=
=0)
return
3
else return Alg(n-1) + Alg(n-1) +
Alg(n-1))
},
wtedy dla n naturalnego:
a)
S(Alg, n)=Θ(n), jeżeli uwzględnimy stos wywołań rekurencyjnych
b) S(Alg, n)=O(n), jeżeli nie uwzględnimy
stos wywołań rekurencyjnych
c)
W(Alg, n)≠ Θ(A(Alg,n))
d)
Alg(n)=3n
e) T(Alg, n)=Ω(3n)
77. Rozpatrujemy
całkowitą poprawność algorytmu, poprzez metodę niezmienników pętli. Jesteśmy w
miejscu, tuż po zakończeniu pętli. Wiemy, że:
a) zachodzi zaprzeczenie dozoru pętli
b) zachodzi zaprzeczenie dozoru pętli oraz
niezmiennik pętli z ostatniej iteracji
c)
zachodzi dozór pętli oraz niezmiennik pętli z ostatniej iteracji
78. Przy
haszowaniu otwartym z uporządkowanymi listami wykonanie k operacji insert do
pustej n-elementowej tablicy:
a) pesymistycznie kosztuje O(k2)
b)
pesymistycznie kosztuje O(n2)
c) średnio kosztuje O(k2/n)
ad1: jeśli haszujemy cały czas pod ten
sam adres
ad2: pesymistycznie kosztuje O(k2), jednak nie da się przeprowadzić
poprawnie haszowania otwartego, jeśli nie mamy miejsca na wszystkie elementy,
więc skoro k<=n, to O(n2) jest dobrym szacowaniem. Z drugiej
strony jeśli nie ma takiego ograniczenia, ani kontroli, to nie jest to dobre
ograniczenie
ad3: ilość możliwych kolizji na wolne miejsce --> wygląda ok
79. Przy założeniu,
że n>
j=n;
x=k;
while(j!=0)
{
x+=j;
j--;
}
poprawnym niezmiennikiem jest:
a)
parzystość zmiennych j oraz x są zawsze różne
b) jeśli pętla wykonała co najmniej 4
obroty, to parzystość x oraz j są takie same, jak cztery obroty pętli wcześniej
c)
x≥0
d) j
≥0
80. Sortowanie
radixsort pozwala posortować n elementów szybciej niż w czasie O(nlogn) m.in.
dzięki temu, że:
NIEopracowane
a)
reprezentacje elementów z sortowanego zbioru mają określoną i stałą ze względu
na n długość liczoną w bitach
b)
algorytm countsort jest stabilny
c)
nie wykonujemy bezpośrednich operacji na elementach, tylko odwołujemy się do
ich reprezentacji bitowej
81. Aby otrzymać
B-drzewo o wysokości 2 dla t=5
a)
wstawić co najwyżej 1000 elementów
b) doprowadzić do sytuacji, w której
łącznie będzie co najmniej 9 węzłów
c)
ustalić jego stopień na co najmniej 5
d)
należy po zainicjalizowaniu pustego drzewa wstawić co najmniej 25 elementów
* by s5002:
ad1: nie jestem na 100% pewna, ale raczej nie - każdy węzeł może mieć do 5 synów
i w każdym węźle jest najwyżej po 4 elementy, więc będzie 4 + 5*(4) + 5*5*(4) =
ad2: na 100% tak (Chrząstowski to ze mną omawiał, zresztą można to sprawdzić na
tym applecie dotyczącym drzew)
ad3: nie (przynajmniej w kluczu tego nie było, bo nie wiem, co oznacza stopień
drzewa)
ad4: na 100% tak (wystarczy 17 elem. - sprawdziłam na applecie)
ode mnie:
zgodnie z Cormenem (wg. którego dr Chrząstowski wykładał B-drzewa) wysokość h
≤ logt((n+1)/2), gdzie t to minimalny stopień B-drzewa (czyli
każdy węzeł poza korzeniem musi mieć co najmniej t-1 i nie więcej niż 2t-1
kluczy)
ad1: po wstawieniu jednej liczby drzewo jest wysokości 0, więc to kiepskie
oszacowanie
ad3: stopień grafu to maksimum po stopniach wierzchołków danego grafu
ad4: jeśli możemy otrzymać drzewo wysokości 2 po wstawieniu 17 elementów, to
chyba nie to samo co po 25. W każdym razie co najmniej 25 to też 2000, co
raczej nie da drzewa wysokości dokładnie 2 więc odznaczam to:)
82. Rozważmy
drzewo T typu AVL powstałe przez losowe wstawianie wierzchołków o etykietach
1,2,3,…., n-1,n do początkowo pustej struktury, wtedy:
a) w drzewie T może istnieć ścieżka
korzeń-liść, której długość jest rzędu O(n1/2)
b) wysokość drzewa T jest nie większa niż
c×n, gdzie c jest pewną stałą
c)
w drzewie T może istnieć ścieżka korzeń-liść, której długość jest rzędu
lg(lg(n))
d) usunięcie pewnego wierzchołka z drzewa T
może wymagać wykonania co najwyżej jednej podwójnej rotacji
e) usunięcie pewnego wierzchołka z drzewa T
może wymagać wykonania Θ(lg(n)) rotacji
f) wstawienie wierzchołka z etykietą n+1 do
drzewa T wymaga wykonania co najwyżej jednej podwójnej rotacji
g)
wstawienie wierzchołka z etykietą n+1 do drzewa T wymaga Θ(n) rotacji
h) wysokość drzewa T jest nie większa niż
c×lg(n), gdzie c jest pewną stałą
* ad1: avl jest drzewem zrównoważonym,
więc wysokość wynosi lgn+/-1, ale lgn < n1/2, więc ścieżka
długości lgn jest rzędu O(n1/2)
ad2: jw. c może być jedynką bo lgn < n
ad3: jw. wysokośc jest rzędu Θ(lgn)
ad4: skoro jest tryb przypuszczający, to czemu nie;) a tak na serio to
przypadków takich jest mnóstwo (np usunięcie liścia dla drzewa avl o 3
wierzchołkach - nie trzeba nic zmieniać)
ad5: O(lgn) jest pesymistycznym ograniczeniem z góry, więc w najbardziej
pesymistycznym przypadku,kiedy trzeba całe drzewo po kolei poziomami
równoważyć, może to być Θ(lg(n)) rotacji
ad6/7: wstawienie do drzewa zawsze wymaga co najwyżej jedną co najwyżej
podwójną rotację
ad8: jak 1/2/3, stała c = 1..2
83. Które z
poniższych zdań jest zawsze prawdziwe w strukturze słowników:
a) ┐member(insert(delete(d,e),e),e)
b) empty(d)↔empty(delete(insert(insert(d,e),e),e))
c) member(insert(delete(d,e),e),e)
d) ┐empty(d) ↔
empty(delete(insert(insert(d,e),e),e))
* ad2: nieprawdziwe, jeśli d składało
się wyłącznie z elementu e
84. Które z
poniższych zdań jest zawsze prawdziwe w strukturze stosów:
a) ┐empty(s)→top(s)≠top(push(pop(s),e))
b) empty(s)→ ┐empty(pop(push(s,e))
c) ┐empty(s)→top(pop(push(s,top(s))))=top(s)
* ad1: jeśli stos ma tylko element e,
to następnik implikacji fałszywy
85. Mamy pewien
algorytm o złożoności obliczeniowej O(n2), zmierzyliśmy czas
działania dla pewnych danych o dużej liczbie elementów, równej n i czas wyniósł
t.
a) Szacunkowo, algorytm w ciągu 4t, jest w
stanie przetworzyć dane o wielkości 2n
b)
Szacunkowo, algorytm w ciągu 16t, jest w stanie przetworzyć dane o wielkości 8n
c) Szacunkowo, algorytm w ciągu 8t, jest w
stanie przetworzyć dane o wielkości 2n
d)
Szacunkowo, algorytm dla danych wielkości 4n, będzie działać 4t.
e) Szacunkowo, algorytm w ciągu 64t, jest w
stanie przetworzyć dane o wielkości 8n
86. Dana jest
funkcja laszująca h(i)=i mod17 oraz rehaszująca r(i)=(i+3)mod17. Korzystając z
tych funkcji wprowadzamy do początkowo pustej tablicy intA[16] kolejno
wartości: 6,0,20,13,3,17. Po wprowadzeniu tych liczb:
a) trzy liczby znajdują się pod indeksami
im równymi
b) 0 poprzedza wszystkie inne wprowadzone
wartości
c)
3 występuje przed 6
d)
17 znajdzie się po wszystkich wprowadzonych wartościach
87. Wyznaczenie
operacji(i) dominującej/ych jest potrzebne do określenia:
a) złożoności optymistycznej pamięciowej
b) złożoności oczekiwanej pamięciowej
c) złożoności oczekiwanej obliczeniowej
* złożoność pamięciowa raczej nie jest określona przez
operacje dominujące. Wyjątkiem są algorytmy rekurencyjne. Biorąc je pod uwagę
zaznaczyłbym wszystko.
88. Analizujemy
częściową poprawność algorytmu. Powinniśmy więc sprawdzić:
a) własność stopu
b)
krok indukcyjny
c) czy niezmiennik pętli jest prawdziwy po
wejściu do pętli dla danych spełniających warunek początkowy
d)
czy niezmiennik pętli jest prawdziwy po wejściu do pętli dla każdych danych wejściowych
* algorytm jest częściowo poprawny,
jeśli dla warunków początkowych się zatrzyma i da wynik spełniający warunek
końcowy lub nie zatrzyma się
89. Niech f(n)=n
2 lg(n), wtedy prawdą jest, że:
a) f(n) × f(n)=Ω(n3)
b) f(n) × f(n)= Θ(n3)
c) f(n) =O(n3)
d) f(n) = Ω (2n)
e) f(n)=Θ (n2)
f) f(n)+f(n)=Θ(n3)
g) f(n)+f(n)=O(n3)
* f(n)=n2lg(n) = n2
90. Pesymistycznie
operacja wyszukiwania elementu w n-elementowym drzewie AVL: Niech f(n)=n 2 lg(n),
wtedy prawdą jest, że:
a)
wymaga Θ(logn) pamięci
b) ma złożoność obliczeniową O(lg n)
c) wymaga Θ(1) pamięci
* po to jest AVL
91. Rozważmy
algorytm Hoare’a wyszukania elementu k-tego co do wielkości w nieuporządkowanym
uniwersum rozmiaru n, wtedy:
a) złożoność pesymistyczna algorytmu jest
rzędu co najmniej n
b)
złożoność średnia algorytmu jest rzędu co najwyżej lg(n)
c)
liczba wywołań procedury podziału (np. Split, Partition) jest rzędu co najwyżej
k
d) złożoność pesymistyczna algorytmu jest
rzędu co najwyżej n2
*ad1: bo musi zajrzeć do wszystkich
danych
ad2: średnio jest linowy
ad3: jeśli mamy pecha, to w pesymistycznym przypadku zawsze wybieramy
największy element, więc wywołujemy split/partition n-1 razy (mając wówczas
kwadratową złożonośc)
ad4: true
92. Niech Alg1
oraz Alg2 będą algorytmami takimi, że T(Alg1,n)=O(nlg(n)) oraz A(Alg2,n)=O(lg(n!)) i W(Alg2,n)=Θ(n3).
Rozważmy teraz algorytm Alg3 taki, że Alg3(n)=
{
int
i=0;
while(i<n)
do
if((i
MOD 2)= =0)
Alg1(i)
else Alg2(i);
i=i+1
od
},
wtedy:
a)
A(Alg3,n)=Θ(n3)
b)
A(Alg3,n)=O(n2)
c) W(Alg3,n)=Ω(n3lg(n))
* alg1 i alg2 wykonujemy mniej więcej
n/2 razy, więc W(alg3)=n(W(alg1)+W(alg2))=n*(O(nlgn)+Θ(n3))=Θ(n4),
A(alg3)=n(A(alg1)+A(alg2))=n(O(nlgn)+O(nlgn))=O(n2lgn)
93. Niech X będzie tablicą n losowych liczb naturalnych
oraz SS, IS, QS będą odpowiednio algorytmami sortowania przez selekcję,
sortowania przez wybór i sortowania szybkiego, wtedy:
a) W(QS(SS(IS(X))),n)= Ω(n)
b) A(IS(QS(X)),n)=O(lg(n!))
c) A(QS(IS(SS(X))),n)=O(n3)
d) W(SS(IS(X)),n)=Θ(n×lg(n))
e)
A(SS(QS(X)),n)=O(n×lg(n))
*ad1: quickSort dla posortowanych
danych działa w czasie O(n2)
ad2: quickSort średnio działa w czasie O(nlgn), a insertionSort działa w czasie
liniowym dla posortowanych danych
ad3: nie znam sortowanie, którego nie można ograniczyćzgóry przez n3
ad4/5: selectionSort działa w czasie Θ(n2)
94. Lepiej użyć
algorytmu InsertionSort, zamiast MergeSort, kiedy…
a) dane są prawie posortowane
b) mamy do czynienia z bardzo małymi danymi
c) mamy bardzo mało dodatkowej pamięci
95. Czym można
posortować dane używając:
a)
sortowania kubełkowego, a w kubełkach posortować dane używając algorytmu
Dijkstry
b)
sortowania kubełkowego, a w kubełkach posortować dane używając Sita
Eratostenesa
c)
RadixSort,a do sortowaia po poszczególnych
kolumnach sortowania kubełkowego, a w kubełkach stabilnej wersji QuickSort
d) sortowania kubełkowego, a w
kubełkach posortować dane używając QuickSort
e) drzewa AVL
*ad 1/2: ani Dijkstra ani sito nie
sortują
ad3: wygląda, że ma ręce i nogi, ale sobie nic nie dam uciąć
96. Który z
podanych poniżej ciągów jest asymptotycznie rosnącym ciągiem funkcji zmiennej n
w dziedzinie liczb naturalnych dodatnich:
a)
2n, (3!)n/2,
(32)n/2, (n/2)!, n!-7n, nn/3
b)
2n-1, lg(lg(n!)), lg(n)-3, n1/3, n3, 2n,
3n-2
c)
lg(n), lg(n!), n2, n2-n, n3+100, lg(n)×n!, n!
*ad1: mała nieścisłość: n!-7n = O(nn),
nn/3=O(nn), więc asympotycznie są sobie równe, a w treści
ciąg ma być rosnący (nieścisłość; czasem w testach jest dokładnie napisane
niemalejący itp. rosnący może być zarówno ściśle rosnący lub niemalejący - to
pewnie można wybronić na ustnych, jeśli jest odznaczony w kluczu)
ad2: lgn-3 < lg(nlgn)
ad3: n! < n!lgn