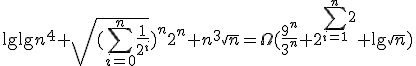1	Rozważmy funkcje zmiennej . Które z poniższych zdań jest prawdziwe?
		0
		0
		1	+
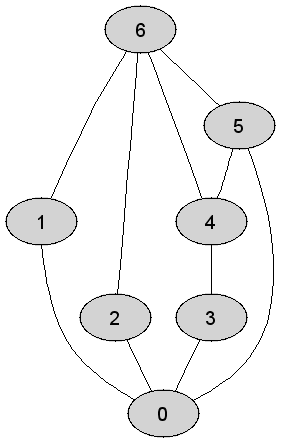
2	Rozważmy drzewo typu AVL powstałe na skutek kolejnego wstawiania elementów ciągu do początkowo pustej struktury (przy użyciu operacji INSERT). Które z poniższych zdań jest prawdziwe?
	Łączna liczba rotacji pojedynczych w prawo wykonanych w trakcie budowy drzewa jest równa dokładnie	0		+
	Łączna liczba rotacji podwójnych w lewo-prawo wykonanych w trakcie budowy drzewa jest równa dokładnie	0
	Łączna liczba rotacji pojedynczych w lewo wykonanych w trakcie budowy drzewa jest równa dokładnie	1	+	+
3	Rozważmy drzewo typu BST powstałe na skutek kolejnego wstawiania elementów ciągu do początkowo pustej struktury (przy użyciu operacji INSERT). Które z poniższych zdań jest prawdziwe?
	Etykiety wierzchołków drzewa wypisane w kolejności PreOrder tworzą ciąg:	1	+	+
	Etykiety wierzchołków drzewa wypisane w kolejności PostOrder tworzą ciąg:	1	+	+
	Etykiety wierzchołków drzewa wypisane w kolejności PreOrder tworzą ciąg:	0
4	Rozważmy pełne drzewo binarne wysokości . Które z poniższych zdań jest prawdziwe?
	Jeżeli wierzchołki drzewa w kolejności PreOrder tworzą ciąg , to w kolejności InOrder tworzą ciąg:	1	+
	Jeżeli wierzchołki drzewa w kolejności InOrder tworzą ciąg , to w kolejności PostOrder tworzą ciąg:	0
	Jeżeli wierzchołki drzewa w kolejności PostOrder tworzą ciąg , to w kolejności InOrder tworzą ciąg:	0
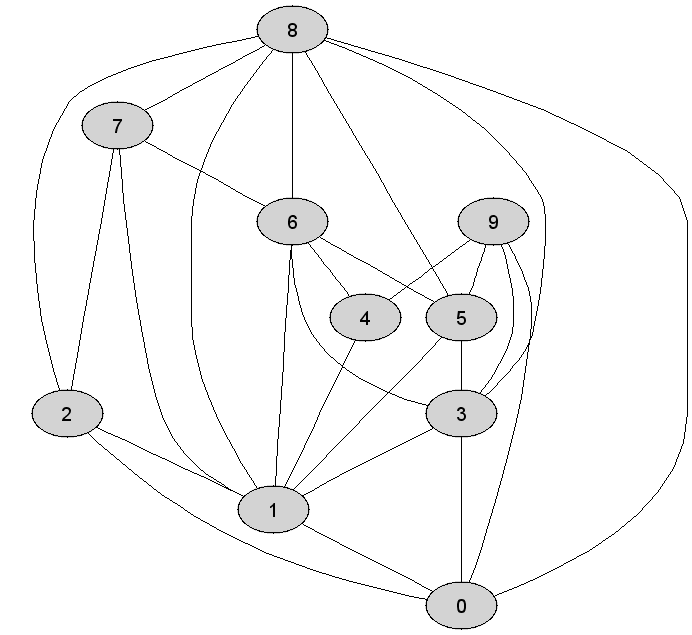
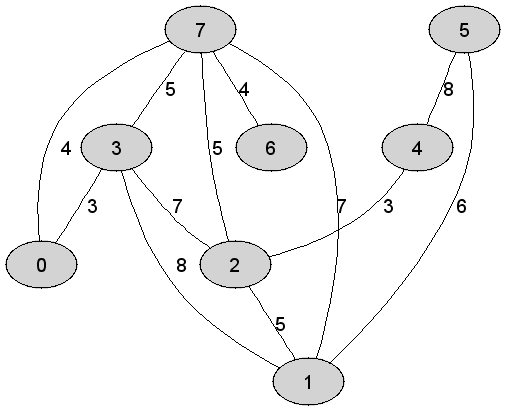
5	Rozważmy nieskierowany graf prosty , którego wierzchołki etykietowane są liczbami naturalnymi od do włącznie, zadany tabicą list sąsiedztwa postaci: , , , , , , , , , i przedstawiony na poniższym rysunku. Dla grafu stosujemy algorytm kolorowania LF (largest first). Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą etykietą. Kolory indeksujemy od .
	Po zastosowaniu algorytm LF wierzchołek ma przypisany taki sam kolor jak wierzchołek	0
	Liczba chromatyczna grafu jest równa dokładnie	1	+	+
	Kolejność kolorowania wierzchołków grafu w trakcie wykonania algorytmu LF jest następująca:	0
6	Rozważmy tablicę reprezentującą -elementowy ciąg liczb naturalnych: . Do posortowania owej tablicy stosujemy algorytm CountingSort. Które z poniższych zdań jest prawdziwe?
	Po drugiej pętli iteracyjnej (sumowanie) postać tablicy pomocniczej wykorzystywanej w rozważanym algorytmie jest następująca:	0
	Po trzeciej pętli iteracyjnej (wypisanie) postać tablicy pomocniczej wykorzystywanej w rozważanym algorytmie jest następująca:	0
	Po trzeciej pętli iteracyjnej (wypisanie) postać tablicy pomocniczej wykorzystywanej w rozważanym algorytmie jest następująca:	1	+
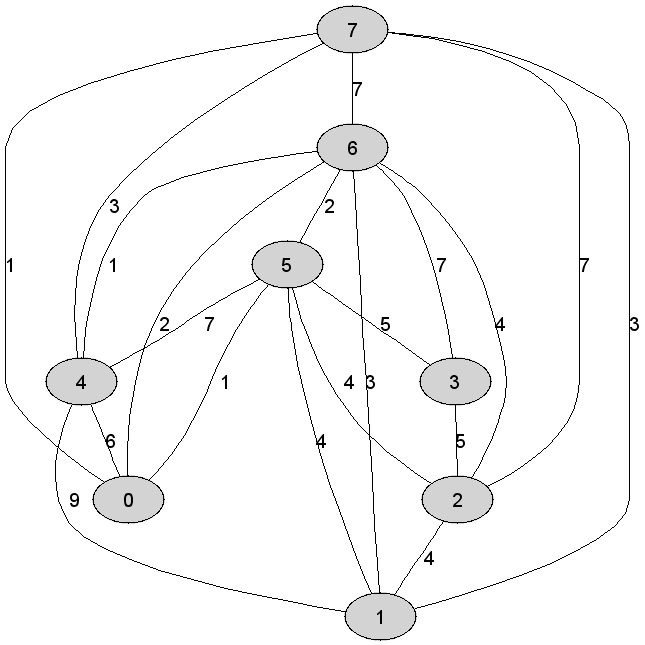
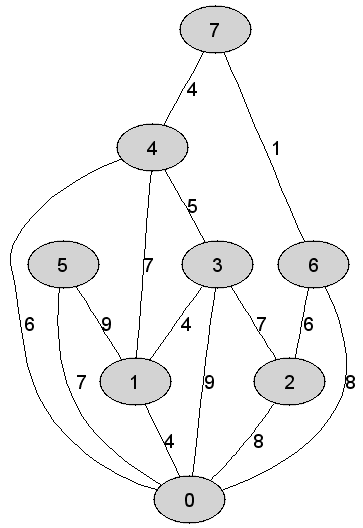
7	Rozważmy nieskierowany graf prosty z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od do włącznie, zadany tabicą list sąsiedztwa postaci: , , , , , , , i przedstawiony na poniższym rysunku. Dla grafu i wierzchołka startowego stosujemy algorytm Dijkstry. Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą etykietą.
	Suma wag krawędzi tworzących drzewo najkrótszych ścieżek będące rezultatem działania algorytmu Dijkstry jest równa dokładnie	0
	Wysokość drzewa najkrótszych ścieżek będącego rezultatem działania algorytmu Dijkstry jest równa dokładnie	1	+	+
	Najkrótsza ścieżka z wierzchołka do wierzchołka w rozważanym grafie jest długości dokładnie	0
8	Rozważmy nieskierowany graf prosty , którego wierzchołki etykietowane są liczbami naturalnymi od do włącznie, zadany tabicą list sąsiedztwa postaci: , , , , , , i przedstawiony na poniższym rysunku. Wierzchołki grafu odwiedzamy w kolejności DFS z wierzchołka startowego . Które z poniższych zdań jest prawdziwe? Uwaga! W algorytmie DFS wierzchołki grafu umieszczamy na stosie pomocniczym w kolejności malejących wartości etykiet.
	Kolejność odwiedzenia wierzchołków jest następująca:	1	+
	Liczba operacji OUT w stosie pomocniczym w trakcie wykonania algorytmu DFS jest równa dokładnie	0
	Liczba operacji PUSH na stosie pomocniczym w trakcie wykonania algorytmu DFS jest równa dokładnie	0
9	Rozważmy kopiec binarny typu min zaimplementowany w drzewie binarnym i powstały na skutek kolejnego wstawiania elementów ciągu do początkowo pustej struktury (przy użyciu operacji INSERT). Które z poniższych zdań jest prawdziwe?
	Jeżeli zamiast drzewa binarnego do implementacji kopca binarnego użyjemy tablicy, to jej finalna postać będzie następująca:	1	+	+
	Liczba wierzchołków wewnętrznych drzewa-kopca jest równa dokładnie	0
	Wysokość drzewa-kopca jest równa dokładnie	0
10	Rozważmy tablicę reprezentującą -elementowy ciąg różnych liczb naturalnych: . W owej tablicy wyszukujemy indeksu elementu -go co do wielkości za pomocą algorytmu Hoare'a z procedurą podziału zgodną z metodą Partition. Które z poniższych zdań jest prawdziwe?
	W rozważanym przypadku liczba wykonanań algorytmu Partition jest równa dokładnie	0
	W rozważanym przypadku liczba wykonanań algorytmu Partition jest większa od liczby wykonań tego algorytmu, gdy zamiast indeksu elementu -go co do wielkości będziemy wyszukiwali indeksu elementu -go co do wielkości	1	+	+
	W rozważanym przypadku liczba wykonanań algorytmu Partition jest równa dokładnie	0
11	Rozważmy drzewo kodowe Huffmana powstałe na skutek zastosowania algorytmu budowy drzewa kodu Huffmana dla ciągu znaków zawierającego odpowiednio (znak - krotność wystąpień): , , , , , , , . Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznego wyboru poddrzew, za mniejsze uznajemy to, którego etykiet liści czytane od lewej do prawej strony tworzą słowo mniejsze w sensie porządku leksykograficznego.
	Kod litery odczytany z drzewa jest następujący:	1	+
	Kod litery odczytany z drzewa jest następujący:	0
	Etykiety liści drzewa czytane od lewej do prawej strony tworzą ciąg	0
12	Rozważmy nieskierowany graf prosty z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od do włącznie, zadany tabicą list sąsiedztwa postaci: , , , , , , , i przedstawiony na poniższym rysunku. Dla grafu stosujemy algorytm Kruskala wyznaczenia minimalnego drzewa rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości wyboru krawędzi, jako pierwszą wybieramy krawędź, której etykiety wierzchołków krańcowych w kolejności niemalejącej tworzą mniejszą liczbę naturalną.
	Maksymalna waga krawędzi tworzącej otrzymane drzewo rozpinające grafu jest równa co najwyżej	1	+
	Liczba krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej postaci, jest równa dokładnie	1	+
	Liczba krawędzi grafu odrzuconych (ze względu na możliwość utworzenia cyklu) w trakcie konstrukcji drzewa rozpinającego, tuż po ustaleniu jego finalnej postaci, jest równa dokładnie	0
13	Rozważmy tablicę reprezentującą -elementowy ciąg różnych liczb naturalnych: . Do posortowania owej tablicy stosujemy algorytm MergeSort w implementacji rekurencyjnej, z procedurą scalania zgodną z metodą Merge. Które z poniższych zdań jest prawdziwe?
	W rozważanym przypadku wyskokść drzewa wywołań rekurencyjnych algorytmu MergeSort jest równa dokładnie	0
	W rozważanym przypadku liczba wykonanań algorytmu Merge jest równa dokładnie	0
	W rozważanym przypadku wyskokść drzewa wywołań rekurencyjnych algorytmu MergeSort jest równa dokładnie	1	+
14	Rozważmy początkowo pustą strukturę kolejki , do której wstawiono elementy: . Następnie na strukturze wykonano kolejno ciąg operacji: , , , , , , , . Które z poniższych zdań jest prawdziwe?
	Ostateczna długość kolejki tuż po wykonaniu przedstawionego ciągu operacji jest taka sama jak w przypadku wykonania następującego ciągu operacji: , , , , , , ,	0
	Ostateczna długość kolejki tuż po wykonaniu przedstawionego ciągu operacji jest równa dokładnie	0
	Maksymalna długość kolejki w trakcie wykonania przedstawionego ciągu operacji jest taka sama jak w przypadku wykonania następującego ciągu operacji: , , , , , , ,	1	+
15	Rozważmy tablicę reprezentującą -elementowy ciąg różnych liczb naturalnych: . Do posortowania owej tablicy stosujemy algorytm QuickSort w implementacji rekurencyjnej, z procedurą podziału zgodną z metodą Partition. Które z poniższych zdań jest prawdziwe?
	W rozważanym przypadku liczba wykonanań rekurencyjnych algorytmu QuickSort jest równa dokładnie	0
	W rozważanym przypadku liczba wykonanań rekurencyjnych algorytmu QuickSort jest równa dokładnie	0
	W rozważanym przypadku liczba wykonanań rekurencyjnych algorytmu QuickSort jest równa dokładnie liczbie wywołań rekurencyjnych rozważanego algorytmu dla danych wejściowych	1	+
16	Rozważmy tablicę reprezentującą -elementowy ciąg -cyfrowych liczb naturalnych: . Do posortowania owej tablicy stosujemy algorytm RadixSort zaimplementowany przy użyciu kolejek. Które z poniższych zdań jest prawdziwe?
	Tuż po sortowaniu liczb względem cyfr na -ej pozycji dziesiętnej (liczonej od prawej do lewej strony), zawartość tablicy jest następująca:	0
	Tuż po sortowaniu liczb względem cyfr na -ej pozycji dziesiętnej (liczonej od prawej do lewej strony), zawartość tablicy jest następująca:	1	+
	Łączna liczba operacji FIRST we wszystkich kolejkach w trakcie wykonania rozważanego algorytmu jest równa dokładnie	0
17	Rozważmy początkowo pustą strukturę stosu , do której wstawiono elementy: . Następnie na strukturze wykonano kolejno ciąg operacji: , , , , , , , . Które z poniższych zdań jest prawdziwe?
	Maksymalna wysokość stosu w trakcie wykonania przedstawionego ciągu operacji jest równa dokładnie	0
	Ostateczna wysokość stosu tuż po wykonaniu przedstawionego ciągu operacji jest taka sama jak w przypadku wykonania następującego ciągu operacji: , , , , , , ,	0
		1	+
18	Rozważmy nieskierowany graf prosty z wagami, którego wierzchołki etykietowane są liczbami naturalnymi od do włącznie, zadany tabicą list sąsiedztwa postaci: , , , , , , , i przedstawiony na poniższym rysunku. Dla grafu i wierzchołka startowego stosujemy stosujemy algorytm Prima wyznaczenia minimalnego drzewa rozpinającego. Które z poniższych zdań jest prawdziwe? Uwaga! W przypadku niejednoznacznej możliwości wyboru wierzchołków, jako pierwszy wybieramy wierzchołek z mniejszą etykietą.
	Liczba wierzchołków wewnętrznych w minimalym drzewie rozpinającym będącym rezultatem działania algorytmu Prima jest równa dokładnie	0
	Suma wag krawędzi tworzących minimalne drzewo rozpinające będące rezultatem działania algorytmu Prima jest równa dokładnie	1	+
	Liczba wierzchołków wewnętrznych w minimalym drzewie rozpinającym będącym rezultatem działania algorytmu Prima jest równa dokładnie	1	+
19	Rozważmy tablicę reprezentującą -elementowy ciąg różnych liczb naturalnych: . Do posortowania owej tablicy stosujemy algorytm SelectionSort. Które z poniższych zdań jest prawdziwe? Uwaga! Przy zliczaniu przestawień elementów bierzemy pod uwagę jedynie transpozycje między różnymi indeksami tablicy .
	Wykonanie pierwszych iteracji pętli zewnętrznej algorytmu wymaga wykonania dokładnie porównań elementów tablicy	1	+
	Wykonanie pierwszych iteracji pętli zewnętrznej algorytmu wymaga wykonania o co najwyżej przestawień elementów tablicy mniej niż w przypadku wykonania pierwszych iteracji rozważanego algorytmu	1	+
	Wykonanie pierwszych iteracji pętli zewnętrznej algorytmu wymaga wykonania dokładnie przestawień elementów tablicy	0
20	Ile maksymalnie elementów można jeszcze umieścić w kopcu, w którym jest już wierzchołków, tak by nie zwiększyć jego wysokości?
	Tyle samo dla , co dla	0
	Tyle samo dla , co dla , dla dowolnego	1	+
	, gdy	0